Ukuran pemusatan data

Ukuran pemusatan data adalah sembarang ukuran yang menunjukkan pusat segugus data, yang telah diurutkan dari yang terkecil sampai yang terbesar atau sebaliknya dari yang terbesar sampai yang terkecil.^[1] Salah satu kegunaan dari ukuran pemusatan data adalah untuk membandingkan dua (populasi) atau contoh, karena sangat sulit untuk membandingkan masing-masing anggota dari masing-masing anggota populasi atau masing-masing anggota data contoh.^[2]. 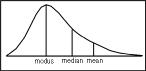Nilai ukuran pemusatan ini dibuat sedemikian sehingga cukup mewakili seluruh nilai pada data yang bersangkutan.^[2]

Data menyebar normal sehingga Median, Mean dan Modus relatif sama

Data menjulur ke kanan sehingga Median, Mean dan Modus berbeda-beda

Ukuran pemusatan yang paling banyak digunakan adalah median, mean, dan modus.^[1]. Masing-masing dari ukuran pemusatan data tersebut memiliki kekurangan.^[1] Nilai tengah akan sangat dipengaruh nilai pencilan.^[1] Median terlalu bervariasi untuk dijadikan parameter populasi.^[1] Sedangkan modus hanya dapat diterapkan dalam data dengan ukuran yang besar.^[1]

Jenis-jenis ukuran pemusatan data

Data tunggal

Mean

merupakan rata-rata hitung

{\bar {x}}={\frac {x_{1}+x_{2}+x_{3}+\cdots +x_{n}}{n}}=\sum \limits _{i=0}^{n}{\frac {x_{i}}{n}}

Median

merupakan nilai tengah setelsh diurutkan

bila ganjil maka terambil di tengah setelah diurutkan. bila genap terambil dua di tengah dibagi rata-rata setelah diurutksn

Me=x_{\frac {n+1}{2}}

bila n ganjil

Me={\frac {x_{\frac {n}{2}}+x_{{\frac {n}{2}}+1}}{2}}

bila n genap

Modus

merupakan nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi

terambil jumlahnya paling banyak setelah diurutkan

Kuartil

merupakan membagi data yang telah menjadi empat bagian yang sama banyak

Q_{i}={\frac {i(n+1)}{4}}

Desil

merupakan membagi data menjadi sepuluh bagian yang sama banyak

D_{i}={\frac {i(n+1)}{10}}

Persentil

merupakan membagi data menjadi seratus bagian yang sama banyak

P_{i}={\frac {i(n+1)}{100}}

Data berkelompok

Dalam data berkelompok terdiri dari tabel, diagram garis, diagram batang serta diagram lingkaran.

Mean

{\bar {x}}={\frac {f_{1}x_{1}+f_{2}x_{2}+f_{3}x_{3}+\cdots +f_{n}x_{n}}{f_{1}+f_{2}+f_{3}+\cdots +f_{n}}}={\frac {\sum \limits _{i=1}^{n}{f_{i}x_{i}}}{\sum \limits _{i=1}^{n}{f_{i}}}}

{\bar {x}}={\bar {x_{s}}}+{\frac {\sum \limits _{i=1}^{n}{f_{i}d_{i}}}{\sum \limits _{i=1}^{n}{f_{i}}}}

{\bar {x}}={\bar {x_{s}}}+({\frac {\sum \limits _{i=1}^{n}{f_{i}u}}{\sum \limits _{i=1}^{n}{f_{i}}}})c

keterangan

f_i = frekuensi untuk nilai i
x_i = data ke-i (untuk data tunggal) atau titik tengah rentang tertentu ke-i (data kelompok)
x_s = titik tengah rataan sementara
d_i = panjang interval antar rentang tertentu pada x_i (di atas $x_{s}$ bernilai min dan dibawah $x_{s}$ bernilai plus)
u = bilangan bulat (jika $x_{s}$ maka u adalah nol. diatasnya min serta dibawahnya plus)
c = panjang interval kelas

Median

Me=L_{2}+({\frac {{\frac {n}{2}}-(\sum {f})_{2}}{f_{Me}}})c

keterangan

$L_{2}$ = tepi bawah kelas median
n = banyak data
$(\sum {f})_{2}$ = jumlah frekuensi sebelum kelas median
$f_{Me}$ = frekuensi kelas median
c = panjang interval kelas

Modus

Mo=L_{o}+({\frac {d_{1}}{d_{1}+d_{2}}})c

keterangan

$L_{o}$ = Tepi bawah kelas modus
$d_{1}$ = selisih frekuensi kelas modus dengan frekuensi kelas sebelum modus
$d_{2}$ = selisih frekuensi kelas modus dengan frekuensi kelas sesudah modus
c = panjang interval kelas

Kuartil

Q_{i}=L_{i}+({\frac {{\frac {in}{4}}-(\sum {f})_{i}}{f_{Q_{i}}}})c

keterangan

i = 1, 2 atau 3
$L_{i}$ = tepi bawah kelas kuartil ke-i
n = banyak data
$(\sum {f})_{i}$ = jumlah frekuensi sebelum kelas kuartil ke-i
$f_{Q_{i}}$ = frekuensi kelas kuartil ke-i
c = panjang interval kelas

Desil

D_{i}=L_{i}+({\frac {{\frac {in}{10}}-(\sum {f})_{i}}{f_{Q_{i}}}})c

keterangan

i = 1, 2, 3, ....., 9
$L_{i}$ = tepi bawah kelas desil ke-i
n = banyak data
$(\sum {f})_{i}$ = jumlah frekuensi sebelum kelas desil ke-i
$f_{Q_{i}}$ = frekuensi kelas desil ke-i
c = panjang interval kelas

Persentil

D_{i}=L_{i}+({\frac {{\frac {in}{100}}-(\sum {f})_{i}}{f_{Q_{i}}}})c

keterangan

i = 1, 2, 3, ....., 99
$L_{i}$ = tepi bawah kelas persentil ke-i
n = banyak data
$(\sum {f})_{i}$ = jumlah frekuensi sebelum kelas persentil ke-i
$f_{Q_{i}}$ = frekuensi kelas persentil ke-i
c = panjang interval kelas

Jenis-jenis ukuran penyebaran data

Lima serangkai

x_{min}

Q_{1}

Q_{2}

Q_{3}

x_{max}

Rataan dua

R_{2}={\frac {Q_{1}+Q_{3}}{2}}

Rataan tiga

R_{3}={\frac {Q_{1}+2Q_{2}+Q_{3}}{2}}

Jangkauan atau Range

R=x_{max}-x_{min}

Jangkauan kuartil

J=Q_{3}-Q_{1}

Jangkauan semi kuartil atau Simpangan kuartil

Q_{d}={\frac {Q_{3}-Q_{1}}{2}}

Simpangan rata-rata

Data tunggal: $SR={\frac {\sum {|x_{i}-{\bar {x}}|}}{n}}$

Data berkelompok: $SR={\frac {\sum \limits _{i=1}^{n}{f_{i}|x_{i}-{\bar {x}}|}}{\sum \limits _{i=1}^{n}{f_{i}}}}$

Ragam atau Varian

Data tunggal: $V={\frac {\sum {|x_{i}-{\bar {x}}|^{2}}}{n}}$

Simpangan baku atau deviasi

Data tunggal: $S={\sqrt {\frac {\sum {|x_{i}-{\bar {x}}|^{2}}}{n}}}$

Lihat pula

Rujukan

^ ^a ^b ^c ^d ^e ^f Ronald E.Walpole. Pengantar Statistika, halaman 22-27". 1993. Jakarta : PT Gramedia Pustaka Utama. ISBN 979-403-313-8
^ ^a ^b Anton Dajan. Pengantar Metode Statistik Jilid I halaman 100-146". 1981. Jakarta : Lembaga Penelitian, Pendidikan dan Penerangan Ekonomi dan Sosial

Artikel bertopik statistika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.

[walpole-1] ^ ^a ^b ^c ^d ^e ^f Ronald E.Walpole. Pengantar Statistika, halaman 22-27". 1993. Jakarta : PT Gramedia Pustaka Utama. ISBN 979-403-313-8

[dajan-2] Anton Dajan. Pengantar Metode Statistik Jilid I halaman 100-146". 1981. Jakarta : Lembaga Penelitian, Pendidikan dan Penerangan Ekonomi dan Sosial

[1]

[2]