Difraksi

Difraksi iyalah penyebaran gelombang, contohnya cahaya, karena adanya halangan. Semakin kecil halangan, penyebaran gelombang semakin besar. Hal ini bisa diterangkan oleh prinsip Huygens. Pada animasi pada gambar sebelah kanan atas terlihat adanya pola gelap dan terang, hal itu disebabkan wavelet-wavelet baru yang terbentuk di dalam celah sempit tersebut saling berinterferensi satu sama lain.

Prinsip Huygens.

Difraksi

Difraksi cahaya diterangkangkan oleh prinsip Huygens.

Difraksi pada dua celah berjarak $d$. Fraksi gelombang putih terjadi pada perpotongan antara garis-garis putih. Fraksi gelombang hitam terjadi pada perpotongan garis-garis berwarna hitam. Fraksi-fraksi gelombang terpisah sejauh sudut $\theta$ dan dirunut dengan urutan $n$.

Untuk menganalisa atau mensimulasikan pola-pola tersebut, dapat digunakan Transformasi Fourier atau disebut juga dengan Fourier Optik.

Difraksi cahaya berturut-turut dipelajari antara lain oleh:

• Isaac Newton dan Robert Hooke pada tahun 1660, sebagai inflexion dari partikel cahaya yang sekarang dikenal sebagai cincin Newton.
• Francesco Maria Grimaldi pada tahun 1665 dan didefinisikan sebagai hamburan fraksi gelombang cahaya ke arah yang berbeda-beda. Istilah yang digunakan saat itu mengambil bahasa Latin diffringere yang berarti to break into pieces.
• James Gregory pada tahun 1673 dengan mengamati pola difraksi pada bulu burung yang kemudian didefinisikan sebagai diffraction grating.
• Thomas Young pada tahun 1803 dan sebagai fenomena interferensi gelombang cahaya. Dari percobaan yang mengamati pola interferensi pada dua celah kecil yang berdekatan, Thomas Young menyimpulkan bahwa kedua celah tersebut lebih merupakan dua sumber gelombang yang berbeda daripada partikel (en:corpuscles).
• Augustin Jean Fresnel pada tahun 1815 dan tahun 1818, dan menghasilkan perhitungan matematis yang membenarkan teori gelombang cahaya yang dikemukakan sebelumnya oleh Christiaan Huygens pada tahun 1690 hingga teori partikel Newton mendapatkan banyak sanggahan. Fresnel mendefinisikan difraksi dari eksperimen celah ganda Young sebagai interferensi gelombang dengan persamaan:

$m\lambda =d\sin \theta$

dimana $d$ adalah jarak antara dua sumber muka gelombang, $\theta$ adalah sudut yang dibentuk antara fraksi muka gelombang urutan ke-$m$ dengan sumbu normal muka gelombang fraksi mula-mula yang mempunyai urutan maksimum $m=0$.. Difraksi Fresnel kemudian dikenal sebagai near-field diffraction, yaitu difraksi yang terjadi dengan nilai $m$ relatif kecil.

• Richard C. MacLaurin pada tahun 1909, dalam monographnya yang berjudul Light, menjelaskan proses perambatan gelombang cahaya yang terjadi pada difraksi Fresnel jika celah difraksi disoroti dengan sinar dari jarak jauh.
• Joseph von Fraunhofer dengan mengamati bentuk gelombang difraksi yang perubahan ukuran akibat jauhnya bidang pengamatan. Difraksi Fraunhofer kemudian dikenal sebagai far-field diffraction.
• Francis Weston Sears pada tahun 1948 untuk menentukan pola difraksi dengan menggunakan pendekatan matematis Fresnel. Dari jarak tegak lurus antara celah pada bidang halangan dan bidang pengamatan serta dengan mengetahui besaran panjang gelombang sinar insiden, sejumlah area yang disebut zona Fresnel (en:Fresnel zone) atau half-period elements dapat dihitung.

Difraksi Fresnel

Geometri difraksi dengan sistem koordinat antara celah pada bidang halangan dan citra pada bidang pengamatan.

Difraksi Fresnel adalah pola gelombang pada titik (x,y,z) dengan persamaan:

$E(x,y,z)={z \over {i\lambda }}\iint {E(x',y',0){\frac {e^{ikr}}{r^{2}}}}dx'dy'$

dimana:

$r={\sqrt {(x-x')^{2}+(y-y')^{2}+z^{2}}}$ , dan

$i\,$ is the satuan imajiner.

Difraksi Fraunhofer

Dalam teori difraksi skalar (en:scalar diffraction theory), Difraksi Fraunhofer adalah pola gelombang yang terjadi pada jarak jauh (en:far field) menurut persamaan integral difraksi Fresnel sebagai berikut:

$U(x,y)={\frac {e^{ikz}e^{{\frac {ik}{2z}}(x^{2}+y^{2})}}{i\lambda z}}\iint _{-\infty }^{\infty }\,u(x',y')e^{-i{\frac {2\pi }{\lambda z}}(x'x+y'y)}dx'\,dy'.$

Persamaan di atas menunjukkan bahwa pola gelombang pada difraksi Fresnel yang skalar menjadi planar pada difraksi Fraunhofer akibat jauhnya bidang pengamatan dari bidang halangan.

Difraksi celah tunggal

Pendekatan numerik dari pola difraksi pada sebuah celah dengan lebar empat kali panjang gelombang planar insidennya.

Grafik dan citra dari sebuah difraksi celah tunggal

Sebuah celah panjang dengan lebar infinitesimal akan mendifraksi sinar cahaya insiden menjadi deretan gelombang circular, dan muka gelombang yang lepas dari celah tersebut akan berupa gelombang silinder dengan intensitas yang uniform.

Secara umum, pada sebuah gelombang planar kompleks yang monokromatik $\Psi ^{\prime }$ dengan panjang gelombang &lambda yang melewati celah tunggal dengan lebar d yang terletak pada bidang x′-y′, difraksi yang terjadi pada arah radial r dapat dihitung dengan persamaan:

$\Psi =\int _{\mathrm {slit} }{\frac {i}{r\lambda }}\Psi ^{\prime }e^{-ikr}\,d\mathrm {slit}$

dengan asumsi sumbu koordinaat tepat berada di tengah celah, x′ akan bernilai dari $-d/2\,$ hingga $+d/2\,$, dan y′ dari 0 hingga $\infty$.

Jarak r dari celah berupa:

$r={\sqrt {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}+z^{2}}}$

$r=z\left(1+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}$

Sebuah celah dengan lebar melebihi panjang gelombang akan mempunyai banyak sumber titik (en:point source) yang tersebar merata sepanjang lebar celah. Cahaya difraksi pada sudut tertentu adalah hasil interferensi dari setiap sumber titik dan jika fase relatif dari interferensi ini bervariasi lebih dari 2π, maka akan terlihat minima dan maksima pada cahaya difraksi tersebut. Maksima dan minima adalah hasil interferensi gelombang konstruktif dan destruktif pada interferensi maksimal.

Difraksi Fresnel/difraksi jarak pendek yang terjadi pada celah dengan lebar empat kali panjang gelombang, cahaya dari sumber titik pada ujung atas celah akan berinterferensi destruktif dengan sumber titik yang berada di tengah celah. Jarak antara dua sumber titik tersebut adalah $\lambda /2$. Deduksi persamaan dari pengamatan jarak antara tiap sumber titik destruktif adalah:

${\frac {d\sin(\theta )}{2}}$

Minima pertama yang terjadi pada sudut &theta minimum adalah:

$d\,\sin \theta _{\text{min}}=\lambda$

Difraksi jarak jauh untuk pengamatan ini dapat dihitung berdasarkan persamaan integral difraksi Fraunhofer menjadi:

$I(\theta )=I_{0}\,\operatorname {sinc} ^{2}(d\sin \theta /\lambda )$

dimana fungsi sinc berupa sinc(x) = sin(px)/(px) if x ? 0, and sinc(0) = 1.

Difraksi celah ganda

Sketsa interferensi Thomas Young pada difraksi celah ganda yang diamati pada gelombang air.

Pada mekanika kuantum, eksperimen celah ganda yang dilakukan oleh Thomas Young menunjukkan sifat yang tidak terpisahkan dari cahaya sebagai gelombang dan partikel. Sebuah sumber cahaya koheren yang menyinari bidang halangan dengan dua celah akan membentuk pola interferensi gelombang berupa pita cahaya yang terang dan gelap pada bidang pengamatan, walaupun demikian, pada bidang pengamatan, cahaya ditemukan terserap sebagai partikel diskrit yang disebut foton.

Pita cahaya yang terang pada bidang pengamatan terjadi karena interferensi konstruktif, saat puncak gelombang (en:crest) berinterferensi dengan puncak gelombang yang lain, dan membentuk maksima. Pita cahaya yang gelap terjadi saat puncak gelombang berinterferensi dengan landasan gelombang (en:trough) dan menjadi minima. Interferensi konstruktif terjadi saat:

${\frac {n\lambda }{a}}={\frac {x}{L}}\quad \Leftrightarrow \quad {n}{\lambda }={\frac {xa}{L}}\;,$

dimana

λ adalah panjang gelombang cahaya

a adalah jarak antar celah, jarak antara titik A dan B pada diagram di samping kanan

n is the order of maximum observed (central maximum is n = 0),

x adalah jarak antara pita cahaya dan central maximum (disebut juga fringe distance) pada bidang pengamatan

L adalah jarak antara celah dengan titik tengah bidang pengamatan

Persamaan ini adalah pendekatan untuk kondisi tertentu. Persamaan matematika yang lebih rinci dari interferensi celah ganda dalam konteks mekanika kuantum dijelaskan pada dualitas Englert-Greenberger.

Difraksi celah majemuk

Difraksi celah ganda (atas) dan difraksi celah 5 dari sinar laser

Difraksi sinar laser pada celah majemuk

Pola difraksi dari sinar laser dengan panjang gelombang 633 nm laser melalui 150 celah

Diagram dari difraksi dengan jarak antar celah setara setengah panjang gelombang yang menyebabkan interferensi destruktif

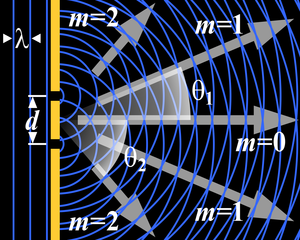
Difraksi celah majemuk (en:Diffraction grating) secara matematis dapat dilihat sebagai interferensi banyak titik sumber cahaya, pada kondisi yang paling sederhana, yaitu yang terjadi pada dua celah dengan pendekatan Fraunhofer, perbedaan jarak antara dua celah dapat dilihat pada bidang pengamatan sebagai berikut:

$\ \Delta S={a}\sin \theta$

Dengan perhitungan maksima:

$\ {a}\sin \theta =n\lambda$		dimana $\ n$ adalah urutan maksima $\ \lambda$ adalah panjang gelombang $\ a$ adalah jarak antar celah and $\ \theta$ adalah sudut terjadinya interferensi konstruktif

Dan persamaan minima:

${a}\sin \theta =\lambda (n+1/2)\,$.

Pada sinar insiden yang membentuk sudut θ_i terhadap bidang halangan, perhitungan maksima menjadi:

$a\left(\sin {\theta _{n}}+\sin {\theta _{i}}\right)=n\lambda .$

Cahaya yang terdifraksi dari celah majemuk dapat dihitung dengan penjumlahan difraksi yang terjadi pada setiap celah berupa konvolusi dari pola difraksi dan interferensi.

Pranala luar

• (Indonesia) Difraksi