Frustum
Dalam geometri, frustum adalah suatu bagian dari bangun ruang seperti kerucut atau limas, yang terletak di antara dua bidang sejajar yang memotongnya. Dalam kasus limas, muka alas berupa poligon, dan muka sisi berupa trapesium. Frustum siku-siku adalah limas siku-siku atau kerucut siku-siku terpenggal, yang tegak lurus dengan garis sumbunya.[1] Bangun terpenggal tersebut yang tidak tegak lurus dengan garis sumbunya disebut frustum bukan siku-siku.
| Kumpulan frustum -gonal siku-siku berbentuk limas | |
|---|---|
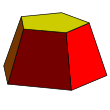  | |
| Muka | trapesium sama kaki, 2 poligon beraturan |
| Rusuk | |
| titik sudut | |
| Polihedron dual | bipiramida segi- siku-siku asimetrik cembung |
| Sifat-sifat | cembung |
Rumus
suntingVolume
suntingRumus volume frustum persegi berbentuk limas diperkenalkan oleh matematika Mesir kuno, yang dikenal sebagai Moskow Matematika Papirus, yang ditulis pada dinasti ke-13 (sekitar 1850 SM): dengan dan masing-masing menyatakan panjang alas dan panjang sisi di atas, serta menyatakan tinggi. Orang Mesir mengetahui rumus yang tepat untuk volume limas persegi penggal, tetapi belum ada bukti dari persamaan tersebut dalam papirus Moskow.
Volume frustum kerucut atau limas merupakan volume bangun ruang sebelum mengiris bagian puncaknya, yang kemudian dikurangi volume bagian puncak: dengan menyatakan luas alas, dan menyatakan luas sisi di bagian atas frustum; serta menyatakan garis tinggi yang tegak lurus dari titik puncak ke alas, dan menyatakan garis tinggi yang tegak lurus dari titik puncak ke sisi di bagian atas frustum. Dengan memisalkan bahwa maka rumus volume dapat dinyatakan sebagai sepertiga hasil kali kesebandingan dan selisih kubik dari dan , yang ditulis sebagai Dengan menggunakan identitas , maka diperoleh dengan menyatakan tinggi frustum. Kemudian, dengan mendistribusikan dan mensubstitusikan dari definisinya, rata-rata Heron dari luas dan akan memberikan rumus volume frustum lainnya, yaitu:
Heron dari Aleksandria adalah seorang matematikawan yang disematkan dengan penemuannya akan rumus volume frustum ini. Dengan menggunakan rumus tersebut, Heron menemukan satuan imajiner, akar kuadrat dari negatif satu.[2]
Secara khusus, volume frustum kerucut melingkar dirumuskan sebagai dengan adalah konstanta yang bernilai 3,14159265...; serta menyatakan jari-jari alas, dan menyatakan jari-jari sisi di bagian atas frustum. Volume frustum limas yang alasnya merupakan poligon (segi- ) beraturan dirumuskan sebagai dengan menyatakan panjang alas dan menyatakan panjang sisi di bagian atas frustum.
Luas permukaan
suntingUntuk frustum kerucut melingkar siku-siku, dipunyai[3] dan dengan menyatakan jari-jari alas, dan menyatakan jari-jari sisi di bagian atas frustum; serta menyatakan garis tinggi miring frustum. Luas permukaan frustum siku-siku yang alasnya merupakan poligon (segi- ) beraturan dirumuskan sebagai dengan dan menyatakan sisi di dua alas frustum.
Lihat pula
suntingReferensi
sunting- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, hlm. 67.
- ^ Nahin, Paul. An Imaginary Tale: The story of √−1. Princeton University Press. 1998
- ^ Al-Sammarraie, Ahmed T.; Vafai, Kambiz (2017). "Heat transfer augmentation through convergence angles in a pipe". Numerical Heat Transfer, Part A: Applications. 72 (3): 197−214. doi:10.1080/10407782.2017.1372670.


