Bentuk kanonik
Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. (December 2007) |
Dalam matematika dan ilmu komputer, bentuk kanonik, normal, atau standar dari objek matematika adalah cara standar untuk menampilkan objek tersebut sebagai ekspresi matematika. Seringkali, itu adalah salah satu yang memberikan representasi paling sederhana dari suatu objek dan yang memungkinkannya untuk diidentifikasi dengan cara unik. Perbedaan antara bentuk "kanonik" dan "normal" bervariasi dari subbidang ke subbidang. Di sebagian besar bidang, bentuk kanonik menentukan representasi unik untuk setiap objek, sedangkan bentuk normal hanya menentukan bentuknya, tanpa persyaratan keunikan.[1]
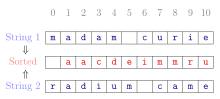
Bentuk kanonik dari bilangan bulat positif dalam representasi desimal adalah barisan digit berhingga yang tidak dimulai dengan nol. Secara umum, untuk kelas objek yang dimana relasi ekuivalensi didefinisikan, sebuah bentuk kanonik terdiri dari pilihan objek tertentu di setiap kelas. Misalnya:
- Bentuk normal Jordan adalah bentuk kanonik untuk keserupaan matriks.
- Bentuk baris eselon adalah bentuk kanonik, ketika menganggap matriks ekuivalen dan hasil kali kirinya dengan matriks invers.
Dalam ilmu komputer, dan secara umum dalam aljabar komputer, ketika mewakili objek matematika di komputer, biasanya ada banyak cara berbeda untuk mewakili objek yang sama. Dalam konteks ini, bentuk kanonik adalah representasi sedemikian rupa sehingga setiap objek memiliki representasi unik (dengan kanonikalisasi menjadi proses yang dimana representasi dimasukkan ke dalam bentuk kanoniknya).[2] Jadi, kesetaraan dua objek dapat dengan mudah diuji dengan menguji kesetaraan bentuk kanoniknya.
Terlepas dari keuntungan ini, bentuk kanonik sering bergantung pada pilihan arbitrer (seperti mengurutkan variabel), yang menimbulkan kesulitan untuk menguji kesetaraan dua objek yang menghasilkan perhitungan yang independen. Oleh karena itu, dalam aljabar komputer, bentuk normal adalah gagasan yang lebih lemah: Sebuah bentuk normal adalah representasi sedemikian rupa sehingga nol direpresentasikan secara unik. Ini memungkinkan pengujian kesetaraan dengan menempatkan perbedaan dua objek dalam bentuk normal.
Bentuk kanonik juga bisa berarti bentuk diferensial yang didefinisikan secara alamiah (kanonik).
Definisi
Diberikan himpunan S objek dengan relasi ekuivalen R pada S, sebuah bentuk kanonik diberikan dengan menunjuk beberapa objek S menjadi "dalam bentuk kanonik", sedemikian rupa sehingga setiap objek yang dipertimbangkan setara dengan tepat satu objek dalam bentuk kanonik. Dengan kata lain, bentuk-bentuk kanonik dalam “S” mewakili kelas-kelas ekuivalen yang hanya sekali. Untuk menguji apakah dua objek ekuivalen, maka cukup menguji kesetaraan pada bentuk kanoniknya. Sebuah bentuk kanonik dengan demikian menyediakan teorema klasifikasi dan sebagainya, dalam hal ini tidak hanya mengklasifikasikan setiap kelas, tetapi juga memberikan perbedaan (kanonik) perwakilan untuk setiap objek di kelas.
Secara formal, kanonikalisasi sehubungan dengan suatu relasi ekuivalensi R pada suatu himpunan S merupakan pemetaan c:S→S sehingga untuk semua s, s1, s2 ∈ S:
- c(s) = c(c(s)) (idempotensi),
- s1 R s2 jika dan hanya jika c(s1) = c(s2) (penegasan), dan
- s R c(s) (keterwakilan).
Properti 3 adalah; berikut dengan penerapan 2 ke 1.
Dalam istilah praktis, seringkali menguntungkan untuk dapat mengenali bentuk-bentuk kanonik. Ada juga pertanyaan algoritmik praktis yang perlu dipertimbangkan: bagaimana cara berpindahnya dari suatu objek tertentu s dalam S pada bentuk kanoniknya s*? Bentuk kanonik umumnya digunakan untuk membuat operasi dengan kelas ekuivalen menjadi sangat efektif. Misalnya, dalam aritmetika modular, bentuk kanonik untuk kelas residu biasanya diambil sebagai bilangan bulat non-negatif terkecil di dalamnya. Operasi pada kelas secara dilakukan dengan menggabungkan perwakilan ini, dan kemudian mengurangi hasilnya menjadi residu non-negatif yang menjadi sedikit. Persyaratan keunikan terkadang dilonggarkan, memungkinkan bentuk menjadi unik hingga beberapa relasi ekuivalen yang lebih baik, seperti memungkinkan untuk menyusun ulang istilah (jika tidak ada pengurutan alami pada istilah).
Bentuk kanonik mungkin hanya berupa konvensi, atau sebuah teorema dalam. Misalnya, polinomial secara konvensional ditulis dengan istilah dalam pangkat menurun: itu biasanya ditulis x2 + x + 30 dibanding x + 30 + x2, meskipun kedua bentuk tersebut mendefinisikan polinomial yang sama. Sebaliknya, keberadaan bentuk kanonik Jordan untuk sebuah matriks adalah sebuah teorema dalam.
Sejarah
Menurut OED dan LSJ, istilah dalam bahasa Inggris canonical berasal dari kata Yunani Kuno kanonikós (κανονικός, "beraturan, menurut aturan") dari kanṓn (κᾰνών, "tongkat, aturan"). Pengertian norm, standard, atau pola dasar telah digunakan dalam banyak disiplin ilmu. Penggunaan matematis dibuktikan dalam surat tahun 1738 dari Logan.[3] Istilah dalam bahasa Jerman: kanonische Form dibuktikan dalam makalah tahun 1846 oleh Eisenstein,[4] kemudian pada tahun yang sama Richelot menggunakan istilah Normalform dalam sebuah makalah,[5] and in 1851 Sylvester writes:[6]
"Saya sekarang melanjutkan ke [...] cara mereduksi fungsi Aljabar menjadi yang paling sederhana dan paling simetris, atau sebagai teman saya yang mengagumkan M. Pertapa mengusulkan untuk memanggil mereka, Canonical forms (bahasa Indonesia: Bentuk kanonik.")
Pada periode yang sama, penggunaan dibuktikan dengan Hesse ("Normalform"),[7] Hermite ("forme canonique"),[8] Borchardt ("forme canonique"),[9] dan Cayley ("canonical form").[10]
Pada tahun 1865, Kamus Sains, Sastra, dan Seni mendefinisikan bentuk kanonis sebagai:
"Dalam matematika, menunjukkan suatu bentuk, biasanya yang paling sederhana atau paling simetris, yang tanpa kehilangan keumumannya, semua fungsi dari kelas yang sama dapat direduksi."
Contoh
Catatan: pada bagian ini, "hingga" beberapa relasi ekuivalen E berarti bahwa bentuk kanonik pada umumnya tidak unik, tetapi jika satu objek memiliki dua bentuk kanonik yang berbeda, keduanya setara dengan E.
Notasi bilangan besar
Bentuk standar digunakan oleh banyak matematikawan dan ilmuwan untuk menulis bilangan besar yang ringkas dan mudah dipahami, yang paling menonjol adalah notasi ilmiah.[11]
Teori bilangan
- Representasi kanonik dari bilangan bulat positif
- Bentuk kanonis dari pecahan kontinu
Aljabar linear
| Objek | A adalah ekuivalen dengan B kalau: | Bentuk normal | Catatan |
|---|---|---|---|
| Matriks normal atas bilangan kompleks. | untuk beberapa matriks satuan U | Matriks diagonal (hingga penataan ulang) | Ini merupakan teorema Spektral |
| Matriks atas bilangan kompleks | untuk beberapa matriks satuan U dan V | Matriks diagonal dengan entri positif rill (dalam urutan menurun) | Dekomposisi nilai singular |
| Matriks atas medan tertutup secara aljabar | untuk beberapa matriks terbalik P | Bentuk normal Jordan (hingga penataan ulang blok) | |
| Matriks atas medan tertutup aljabar | untuk beberapa matriks terbalik P | Bentuk kanonik Weyr (hingga penataan ulang blok) | |
| Matriks atas medan | untuk beberapa matriks terbalikP | Bentuk normal Frobenius | |
| Matriks pada ranah ideal utama | untuk beberapa matriks terbalik P dan Q | Bentuk normal Smith | Persamaannya sama dengan memungkinkan transformasi baris dan kolom elementer terbalik |
| Matriks atas bilangan bulat | untuk beberapa matriks unimodular U | Bentuk normal Hermite | |
| Matriks atas bilangan bulat modulo n | Bentuk normal Howell | ||
| Ruang vektor berdimensi-hingga atas medan K | A dan B adalah isomorfik sebagai ruang vektor | , n sebuah bilangan bulat non-negatif |
Aljabar
| Objek | A adalah ekuivalen dengan B kalau: | Bentuk normal |
|---|---|---|
| Modul-R yang dihasilkan halus dengan R adalah sebuah ranah ideal utama | A dan B adalah isomorfik sebagai modul-R | Dekomposisi primer (hingga penyusunan ulang) atau dekomposisi faktor invarian |
Geometri
Dalam geometri analitik:
- Persamaan sebuah garis: Ax + By = C, dengan A2 + B2 = 1 dan C ≥ 0
- Persamaan sebuah lingkaran:
Sebaliknya, ada bentuk alternatif untuk menulis persamaan. Misalnya, persamaan garis dapat ditulis sebagai persamaan linear dalam titik-kemiringan dan bentuk potongan-kemiringan.
Polihedra cembung dapat dimasukkan ke dalam bentuk kanonik sehingga:
- Semua muka datar,
- Seluruh sisi bersinggungan dengan satuan bola, dan
- Pusat massa polihedra berada pada titik asal.[12]
Sistem terintegralkan
Setiap manifold yang bisa dibedakan memiliki berkas kotangen. Berkas tersebut selalu diberikan dengan bentuk diferensial tertentu, yang disebut bentuk satu kanonik. Bentuk ini memberikan berkas kotangen struktur manifold simplektis, dan memungkinkan medan vektor pada manifold untuk diintegrasikan melalui persamaan Euler-Lagrange, atau melalui mekanika Hamiltonian. Sistem persamaan diferensial yang bisa diintegralkan disebut sistem terintegralkan.
Sistem dinamikal
Studi tentang sistem dinamikal tumpang tindih dengan sistem terintegralkan; terdapat ada gagasan tentang bentuk normal (sistem dinamis).
Geometri tiga dimensi
Dalam mempelajari manifold dalam tiga dimensi, kita memiliki bentuk dasar pertama, bentuk dasar kedua dan bentuk dasar ketiga.
Analisis fungsional
| Objek-objek | A setara dengan B jika: | Bentuk normal |
|---|---|---|
| Ruang Hilbert | Jika A dan B adalah kedua ruang Hilbert dari dimensi tak hingga, maka A dan B adalah isomorfik isometrik. | Ruang urutan (hingga menukar kumpulan indeks I dengan kumpulan indeks lain dari kardinalitas yang sama) |
| Komutatif C*-aljabar dengan satuan | A dana B adalah isomorfik sebagai C*-aljabar | Aljabar dari fungsi kontinyu pada sebuah ruang Hausdorff kompak, hingga homeomorfisme dari basis ruang tersebut. |
Logika klasik
- Bentuk normal negasi
- Bentuk normal konjungtif
- Bentuk normal disjungtif
- Bentuk normal aljabar
- Bentuk normal preneks
- Bentuk normal skolem
- Bentuk kanonik Blake, juga dikenal sebagai jumlah lengkap implikan prima, jumlah lengkap, atau bentuk prima disjungtif
Teori himpunan
Teori permainan
Teori bukti
Menulis ulang sistem
Manipulasi simbolik suatu rumus dari satu bentuk ke lainnya disebut "penulisan ulang" dari rumus itu. Seseorang dapat mempelajari sifat abstrak dari penulisan ulang rumus generik, dengan mempelajari kumpulan aturan dengan rumus yang dapat dimanipulasi secara valid. Ini adalah "aturan penulisan ulang"—bagian integral dari sistem penulisan ulang abstrak. Pertanyaan umum adalah apakah itu mungkin untuk membawa beberapa ekspresi umum ke satu bentuk umum, bentuk normal. Jika rangkaian penulisan ulang yang berbeda masih menghasilkan bentuk yang sama, maka bentuk tersebut dapat disebut bentuk normal, dengan penulisan ulang disebut konfluen. Tidak selalu mungkin untuk mendapatkan bentuk normal.
Kalkulus Lambda
- Istilah lambda ada di bentuk normal beta jika tidak ada kemungkinan pengurangan beta; kalkulus lambda adalah kasus khusus dari sistem penulisan ulang abstrak. Dalam kalkulus lambda yang tidak diketik, misalnya, istilah tidak memiliki bentuk normal. Dalam kalkulus lambda yang diketik, setiap istilah yang terbentuk dengan baik dapat ditulis ulang ke bentuk normalnya.
Teori graf
Dalam teori graf, cabang matematika yaitu kanonisasi graf adalah masalah menemukan bentuk kanonis dari graf tertentu G. Bentuk kanonis adalah label graf Canon(G) yaitu isomorfik menjadi G, sehingga setiap graf isomorfis terhadap G memiliki bentuk kanonis yang sama dengan G. Jadi, dari solusi untuk masalah kanonisasi graf, bisa menyelesaikan masalah isomorfisme graf: untuk menelaahnya apakah dua graf G dan H adalah isomorfik, dari hitung bentuk kanonisnya Canon(G) dan Canon(H), dan telaah apakah kedua bentuk kanonis ini identik.
Komputasi
Dalam komputasi, reduksi data menjadi bentuk kanonis secara biasanya disebut normalisasi data.
Misalnya, normalisasi basis data adalah proses pengorganisasian medan, dan tabel dari basis data relasional untuk meminimalkan redundansi dan ketergantungan.[13]
Di bidang keamanan perangkat lunak, kerentanan adalah input berbahaya yang tidak periksa (lihat injeksi kode). Mitigasi untuk masalah ini sudah tepat validasi input. Sebelum validasi input dilakukan, input biasanya dinormalisasi dengan menghilangkan pengkodean (yaitu, Pengkodean HTML), dan mengurangi data masukan menjadi satu kumpulan karakter umum.
Bentuk data lain, biasanya terkait dengan pemrosesan sinyal (termasuk audio, dan pencitraan) atau pembelajaran mesin, dapat dinormalisasi untuk memberikan rentang nilai yang terbatas.
Dalam manajemen konten, konsep sumber kebenaran tunggal (SSOT) dapat diterapkan, seperti dalam normalisasi basis data secara umum dan dalam pengembangan perangkat lunak. Sistem manajemen konten yang kompeten menyediakan cara logis untuk mendapatkannya, seperti transklusi.
Lihat pula
Catatan
- ^ Dalam beberapa kesempatan, istilah "kanonik" dan "normal" juga dapat digunakan secara bergantian, seperti dalam bentuk kanonik Jordan dan bentuk normal Jordan (lihat Bentuk normal Jordan di MathWorks).
- ^ Istilah 'kanonisasi' terkadang salah digunakan untuk ini.
- ^ "Letter from James Logan to William Jones, Correspondence of Scientific Men of the Seventeenth Century" (dalam bahasa Inggris). University Press. 1841.
- ^ "Journal für die reine und angewandte Mathematik 1846". de Gruyter.
- ^ Journal für die reine und angewandte Mathematik 1846. de Gruyter.
- ^ "The Cambridge and Dublin mathematical journal 1851". Macmillan.
- ^ Hesse, Otto (1865). "Vorlesungen aus der analytischen Geometrie der geraden Linie, des Punktes und des Kreises in der Ebene" (dalam bahasa German). Teubner.
- ^ "The Cambridge and Dublin mathematical journal 1854" (dalam bahasa Inggris). 1854.
- ^ "Journal für die reine und angewandte Mathematik, 1854". de Gruyter.
- ^ Cayley, Arthur (1889). "The Collected Mathematical Papers" (dalam bahasa Inggris). University.
- ^ "Big Numbers and Scientific Notation". Teaching Quantitative Literacy (dalam bahasa Inggris). Diakses tanggal 2019-11-20.
- ^ Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, 152, Springer-Verlag, hlm. 117–118, ISBN 0-387-94365-X
- ^ "Description of the database normalization basics". support.microsoft.com. Diakses tanggal 2019-11-20.
Referensi
- Shilov, Georgi E. (1977), Silverman, Richard A., ed., Linear Algebra, Dover, ISBN 0-486-63518-X.
- Hansen, Vagn Lundsgaard (2006), Functional Analysis: Entering Hilbert Space, World Scientific Publishing, ISBN 981-256-563-9.