Difraksi

.

Difraksi cahaya diterangkangkan oleh prinsip Huygens.

Difraksi Fraunhofer

Dalam teori difraksi skalar (en:scalar diffraction theory), Difraksi Fraunhofer adalah pola gelombang yang terjadi pada jarak jauh (en:far field) menurut persamaan integral difraksi Fresnel sebagai berikut:

U(x,y)={\frac {e^{ikz}e^{{\frac {ik}{2z}}(x^{2}+y^{2})}}{i\lambda z}}\iint _{-\infty }^{\infty }\,u(x',y')e^{-i{\frac {2\pi }{\lambda z}}(x'x+y'y)}dx'\,dy'.

^[1]

Persamaan di atas menunjukkan bahwa pola gelombang pada difraksi Fresnel yang skalar menjadi planar pada difraksi Fraunhofer akibat jauhnya bidang pengamatan dari bidang halangan.

Difraksi celah tunggal

Pendekatan numerik dari pola difraksi pada sebuah celah dengan lebar empat kali panjang gelombang planar insidennya.

Grafik dan citra dari sebuah difraksi celah tunggal

Sebuah celah panjang dengan lebar infinitesimal akan mendifraksi sinar cahaya insiden menjadi deretan gelombang circular, dan muka gelombang yang lepas dari celah tersebut akan berupa gelombang silinder dengan intensitas yang uniform.

Secara umum, pada sebuah gelombang planar kompleks yang monokromatik $\Psi ^{\prime }$ dengan panjang gelombang &lambda yang melewati celah tunggal dengan lebar d yang terletak pada bidang x′-y′, difraksi yang terjadi pada arah radial r dapat dihitung dengan persamaan:

\Psi =\int _{\mathrm {slit} }{\frac {i}{r\lambda }}\Psi ^{\prime }e^{-ikr}\,d\mathrm {slit}

dengan asumsi sumbu koordinaat tepat berada di tengah celah, x′ akan bernilai dari $-d/2\,$ hingga $+d/2\,$ , dan y′ dari 0 hingga $\infty$ .

Jarak r dari celah berupa:

r={\sqrt {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}+z^{2}}}

r=z\left(1+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}

Sebuah celah dengan lebar melebihi panjang gelombang akan mempunyai banyak sumber titik (en:point source) yang tersebar merata sepanjang lebar celah. Cahaya difraksi pada sudut tertentu adalah hasil interferensi dari setiap sumber titik dan jika fase relatif dari interferensi ini bervariasi lebih dari 2π, maka akan terlihat minima dan maksima pada cahaya difraksi tersebut. Maksima dan minima adalah hasil interferensi gelombang konstruktif dan destruktif pada interferensi maksimal.

Difraksi Fresnel/difraksi jarak pendek yang terjadi pada celah dengan lebar empat kali panjang gelombang, cahaya dari sumber titik pada ujung atas celah akan berinterferensi destruktif dengan sumber titik yang berada di tengah celah. Jarak antara dua sumber titik tersebut adalah $\lambda /2$ . Deduksi persamaan dari pengamatan jarak antara tiap sumber titik destruktif adalah:

{\frac {d\sin(\theta )}{2}}

Minima pertama yang terjadi pada sudut &theta minimum adalah:

d\,\sin \theta _{\text{min}}=\lambda

Difraksi jarak jauh untuk pengamatan ini dapat dihitung berdasarkan persamaan integral difraksi Fraunhofer menjadi:

I(\theta )=I_{0}\,\operatorname {sinc} ^{2}(d\sin \theta /\lambda )

dimana fungsi sinc berupa sinc(x) = sin(px)/(px) if x ? 0, and sinc(0) = 1.

Difraksi celah ganda

Sketsa interferensi Thomas Young pada difraksi celah ganda yang diamati pada gelombang air.^[2]

Pada mekanika kuantum, eksperimen celah ganda yang dilakukan oleh Thomas Young menunjukkan sifat yang tidak terpisahkan dari cahaya sebagai gelombang dan partikel. Sebuah sumber cahaya koheren yang menyinari bidang halangan dengan dua celah akan membentuk pola interferensi gelombang berupa pita cahaya yang terang dan gelap pada bidang pengamatan, walaupun demikian, pada bidang pengamatan, cahaya ditemukan terserap sebagai partikel diskrit yang disebut foton.^[3]^[4]

Pita cahaya yang terang pada bidang pengamatan terjadi karena interferensi konstruktif, saat puncak gelombang (en:crest) berinterferensi dengan puncak gelombang yang lain, dan membentuk maksima. Pita cahaya yang gelap terjadi saat puncak gelombang berinterferensi dengan landasan gelombang (en:trough) dan menjadi minima. Interferensi konstruktif terjadi saat:

{\frac {n\lambda }{a}}={\frac {x}{L}}\quad \Leftrightarrow \quad {n}{\lambda }={\frac {xa}{L}}\;,

dimana

λ adalah panjang gelombang cahaya

a adalah jarak antar celah, jarak antara titik A dan B pada diagram di samping kanan

n is the order of maximum observed (central maximum is n = 0),

x adalah jarak antara pita cahaya dan central maximum (disebut juga fringe distance) pada bidang pengamatan

L adalah jarak antara celah dengan titik tengah bidang pengamatan

Persamaan ini adalah pendekatan untuk kondisi tertentu.^[5] Persamaan matematika yang lebih rinci dari interferensi celah ganda dalam konteks mekanika kuantum dijelaskan pada dualitas Englert-Greenberger.

Difraksi celah majemuk

Difraksi celah ganda (atas) dan difraksi celah 5 dari sinar laser

Difraksi sinar laser pada celah majemuk

Pola difraksi dari sinar laser dengan panjang gelombang 633 nm laser melalui 150 celah

Diagram dari difraksi dengan jarak antar celah setara setengah panjang gelombang yang menyebabkan interferensi destruktif

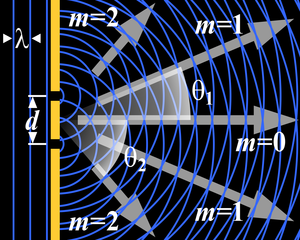
Difraksi celah majemuk (en:Diffraction grating) secara matematis dapat dilihat sebagai interferensi banyak titik sumber cahaya, pada kondisi yang paling sederhana, yaitu yang terjadi pada dua celah dengan pendekatan Fraunhofer, perbedaan jarak antara dua celah dapat dilihat pada bidang pengamatan sebagai berikut:

\ \Delta S={a}\sin \theta

Dengan perhitungan maksima:

$\ {a}\sin \theta =n\lambda$		dimana $\ n$ adalah urutan maksima $\ \lambda$ adalah panjang gelombang $\ a$ adalah jarak antar celah and $\ \theta$ adalah sudut terjadinya interferensi konstruktif

Dan persamaan minima:

{a}\sin \theta =\lambda (n+1/2)\,

.

Pada sinar insiden yang membentuk sudut θ_i terhadap bidang halangan, perhitungan maksima menjadi:

a\left(\sin {\theta _{n}}+\sin {\theta _{i}}\right)=n\lambda .

Cahaya yang terdifraksi dari celah majemuk dapat dihitung dengan penjumlahan difraksi yang terjadi pada setiap celah berupa konvolusi dari pola difraksi dan interferensi.

Referensi

^ Goodman, Joseph (2005). Introduction to Fourier Optics. Englewood, Co: Roberts & Company. ISBN 0-97470777-2-4 Periksa nilai: length |isbn= (bantuan).
^ Rothman, Tony (2003). Everything's Relative and Other Fables in Science and Technology. New Jersey: Wiley. ISBN 0471202576.
^ Feynman, Richard P. (1965). The Feynman Lectures on Physics, Vol. 3. USA: Addison-Wesley. hlm. p.1–8. ISBN 0201021188P Periksa nilai: invalid character |isbn= (bantuan). Pemeliharaan CS1: Teks tambahan (link)
^ Darling, David (2007). "Wave - Particle Duality". The Internet Encyclopedia of Science. The Worlds of David Darling. Diakses tanggal 2008-10-18.
^ For a more complete discussion, with diagrams and photographs, see Arnold L Reimann, Physics, chapter 38.

Pranala luar

(Indonesia) Difraksi

[Goodman-1] Goodman, Joseph (2005). Introduction to Fourier Optics. Englewood, Co: Roberts & Company. ISBN 0-97470777-2-4 Periksa nilai: length |isbn= (bantuan).

[2] Rothman, Tony (2003). Everything's Relative and Other Fables in Science and Technology. New Jersey: Wiley. ISBN 0471202576.

[3] Feynman, Richard P. (1965). The Feynman Lectures on Physics, Vol. 3. USA: Addison-Wesley. hlm. p.1–8. ISBN 0201021188P Periksa nilai: invalid character |isbn= (bantuan). Pemeliharaan CS1: Teks tambahan (link)

[4] Darling, David (2007). "Wave - Particle Duality". The Internet Encyclopedia of Science. The Worlds of David Darling. Diakses tanggal 2008-10-18.

[5] For a more complete discussion, with diagrams and photographs, see Arnold L Reimann, Physics, chapter 38.

[1]

[2]

[3]

[4]

[5]