Diagram kotak garis
Dalam statistika deskriptif, diagram kotak garis atau boxplot adalah metode grafis untuk menggambarkan kumpulan data numerik berdasarkan nilai kuartilnya.[1] Diagram kotak garis bersifat nonparametrik, artinya diagram ini menampilkan variasi sampel populasi statistik tanpa membuat asumsi apa pun tentang distribusi statistik yang mendasarinya. Jarak antara bagian-bagian kotak yang berbeda menunjukkan derajat dispersi (sebaran), kemiringan, dan pencilan dari data tersebut. Diagram kotak garis dapat digambarkan secara horizontal maupun vertikal.
Elemen diagram kotak garis
suntingDiagram kotak garis merupakan salah satu cara sederhana untuk menampilkan kumpulan data berdasarkan ringkasan lima angka dari data tersebut. Ringkasan lima angka yang dimaksud yakni:
Minimum : nilai terendah dari kumpulan data, tidak termasuk pencilan.
Maksimum : nilai terbesar dari kumpulan data, tidak termasuk pencilan.
Median (Q2 / persentil ke-50): nilai tengah kumpulan data.
Kuartil pertama (Q1 / persentil ke-25): juga dikenal sebagai kuartil bawah qn(0.25), adalah median dari bagian bawah kumpulan data.
Kuartil ketiga (Q3 / persentil ke-75): juga dikenal sebagai kuartil qn(0.75), adalah median dari bagian atas kumpulan data.[2]
Elemen penting lain dalam pembuatan diagram kotak garis adalah jangkauan interkuartil (Interquartile range, IQR). Jangkauan interkuartil adalah jarak antara kuartil atas dan bawah, dinotasikan sebagai:
Diagram kotak garis terdiri atas dua bagian, yakni sebuah kotak dan satu pasang garis (seperti pada Gambar 2). Titik terendah dalam diagram merupakan nilai minimum dari dataset, sementara titik tertingginya merupakan nilai maksimum dari dataset. Sebuah kotak digambar dari Q1 ke Q3 kemudian garis horizontal digambar di tengahnya untuk menunjukkan median.
kumpulan data yang sama juga dapat direpresentasikan sebagai diagram kotak garis seperti yang ditunjukkan pada Gambar 3. Pertama, lakukan pengukuran sejauh 1,5 kali IQR dari kuartil atas. Kemudian sebuah garis ditarik dari kuartil atas menuju nilai terbesar dalam dataset yang berada dalam jarak 1,5 kali IQR. Hal yang sama juga dilakukan pada bagian bawah. Sebuah garis ditarik dari kuartil bawah menuju nilai terkecil dalam dataset yang berada dalam jarak 1,5 kali IQR, diukur dari bawah kuartil bawah. Semua titik lainnya dianggap sebagai pencilan.[3]
Meskipun demikian, garis dalam diagram ini dapat mewakili beberapa kemungkinan nilai lainnya, seperti:
- minimum dan maksimum dari semua data (seperti pada gambar 2)
- satu deviasi standar di atas dan di bawah rata-rata data
- persentil ke-9 dan persentil ke-91
- persentil ke-2 dan persentil ke-98.
Data apapun yang tidak termasuk dalam garis harus diplot sebagai pencilan dengan simbol titik, lingkaran kecil, atau bintang, meskipun terkadang hal ini tidak dilakukan. Selain itu, beberapa diagram kotak turut menyertakan simbol tambahan untuk menunjukkan nilai rata-rata data.[4][5]
Variasi
suntingDiagram ini telah memiliki banyak variasi sejak dipopulerkan oleh matematikawan John W. Tukey pada tahun 1969. Dua varian paling umum adalah diagram kotak lebar variabel dan plot kotak berlekuk (lihat Gambar 4).
Plot kotak lebar variabel menggambarkan ukuran setiap grup yang datanya sedang diplot dengan membuat lebar kotak proporsional dengan ukuran grup. Konvensi yang populer adalah membuat lebar kotak proporsional dengan akar kuadrat dari ukuran grup.[6]
Contoh
suntingContoh diagram kotak garis tanpa pencilan
suntingTemperatur udara di suatu tempat diukur tiap jam dalam satuan Fahrenheit. Temperatur yang terukur kemudian disajikan dalam urutan data: 50, 50, 55, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
Sebuah diagram kotak garis kemudian dibuat menggunakan patokan nilai minimum, maksimum, median, kuartil pertama, dan kuartil ketiga dari data temperatur tersebut.
Pada kasus ini, temperatur minimum hari itu adalah 50 °F, maksimum 81 °F, dan median temperatur 70 °F. Kuartil pertama / kuartil bawah data adalah 66 °F, yang mana merupakan nilai tengah antara 50 °F (nilai minimum) dan 70 °F (median). Nilai kuartil ketiga / kuartil atas data temperatur adalah 75 °F, yang mana merupakan nilai tengah antara 70 °F (median) dan 81 °F (maksimum).
Jangkauan interkuartil, atau IQR, kemudian dapat dihitung:
Oleh karena itu, didapatkan bahwa
1.5 IQR di atas kuartil ketiga adalah:
Sementara 1.5IQR di bawah kuartil pertama adalah:
Garis bagian atas dari diagram kotak garis memanjang dari kuartil ketiga hingga nilai data terbesar yang lebih kecil dari 1.5IQR di atas kuartil ketiga. Pada persoalan ini, 1,5IQR di atas kuartil ketiga adalah 88,5 °F dan nilai maksimum yang berada dalam rentang tersebut adalah 81 °F. Oleh karena itu, garis bagian atas digambar dari kuartil ketiga hingga 81 °F.
Serupa dengan garis bagian atas, garis bagian bawah dari diagram kotak garis memanjang dari kuartil pertama hingga nilai data terkecil yang lebih besar dari 1.5IQR di bawah kuartil pertama. Pada persoalan ini, 1,5IQR di bawah kuartil pertama adalah 52,5 °F dan nilai minimum yang memenuhi adalah 55 °F. Dengan demikian, garis bagian bawah digambar dari kuartil pertama hingga 55 °F.
Contoh dengan pencilan
suntingPada contoh ini, diberikan kumpulan data terurut: 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89. Nilai median, kuartil pertama, dan kuartil ketiga sama dengan contoh sebelumnya. Sementara itu, ditambahkan data tambahan pada awal dan akhir sehingga nilai minimum dan maksimumnya berubah menjadi 52 dan 89 berturut-turut.
Pada persoalan ini, nilai maksimum kumpulan data adalah 89 °F, sementara 1.5IQR di atas kuartil ketiga adalah 88,5 °F. Karena nilai maksimum lebih besar daripada kuartil ketiga ditambah 1.5IQR, maka nilai maksimum merupakan pencilan. Oleh karena itu, garis bagian atas digambar hingga nilai terbesar yang lebih kecil dari 1,5IQR di atas kuartil ketiga, yaitu 79 °F.
Hal yang serupa juga berlaku pada bagian bawah. Nilai minimum kumpulan data ini adalah 52 °F, sementara 1.5IQR di bawah kuartil pertama adalah 52.5 °F. Karena nilai minimum lebih kecil daripada 1.5IQR dikurangi kuartil pertama, maka minimum juga merupakan pencilan. Oleh karena itu, garis bawah digambar pada nilai terkecil yang lebih besar dari 1,5IQR di bawah kuartil pertama, yaitu 57 °F.
Dalam kasus kumpulan data besar
suntingPersamaan umum untuk menghitung kuantil empiris
suntingContoh data di atas merupakan kumpulan data dengan 24 titik data, artinya n = 24. Anda juga dapat menghitung median, kuartil pertama, dan kuartil ketiga secara matematis:
Median :
Kuartil pertama :
Kuartil ketiga :
Visualisasi
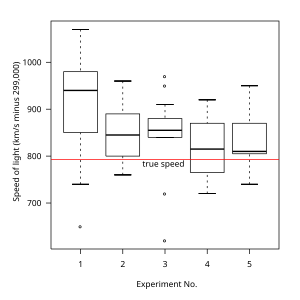
suntingDiagram kotak garis memungkinkan pemeriksaan grafis yang cepat dari satu atau lebih kumpulan data. Diagram kotak garis mungkin tampak lebih primitif daripada histogram atau perkiraan kerapatan kernel. Meskipun demikian, diagram ini membutuhkan lebih sedikit ruang sehingga sangat berguna untuk membandingkan distribusi antara beberapa kelompok atau kumpulan data (lihat Gambar 1 sebagai contoh). Pemilihan teknik jumlah dan lebar batang dapat sangat memengaruhi tampilan histogram, sementara pilihan lebar pita dapat sangat memengaruhi tampilan perkiraan kepadatan kernel.
Salah satu cara untuk memahami diagram kotak garis adalah membandingkannya dengan fungsi kepadatan probabilitas (histogram teoritis) untuk distribusi normal N (0,σ2). Hal ini karena distribusi statistik lebih umum ditemukan daripada diagram kotak (Gambar 7).
Lihat pula
suntingReferensi
sunting- ^ Mason, Robert D.; Lind, Douglas A. Teknik Statistika untuk BISNIS & EKONOMI. Diterjemahkan oleh Sitompul, Ellen Gunawan. Jakarta: Penerbit Erlangga. hlm. 148–150. ISBN 979-411-387-5.
- ^ Holmes, Alexander; Illowsky, Barbara; Dean, Susan. "Introductory Business Statistics". OpenStax. Diarsipkan dari versi asli tanggal 2020-07-27. Diakses tanggal 2020-08-22.
- ^ Dekking, F.M. (2005). A Modern Introduction to Probability and Statistics . Springer. hlm. 234–238. ISBN 1-85233-896-2.
- ^ Frigge, Michael; Hoaglin, David C.; Iglewicz, Boris (February 1989). "Some Implementations of the Boxplot". The American Statistician. 43 (1): 50–54. doi:10.2307/2685173. JSTOR 2685173.
- ^ Marmolejo-Ramos, F.; Tian, S. (2010). "The shifting boxplot. A boxplot based on essential summary statistics around the mean". International Journal of Psychological Research. 3 (1): 37–46. doi:10.21500/20112084.823.
- ^ McGill, Robert; Tukey, John W.; Larsen, Wayne A. (February 1978). "Variations of Box Plots". The American Statistician. 32 (1): 12–16. doi:10.2307/2683468. JSTOR 2683468.
Bacaan lebih lanjut
sunting- John W. Tukey (1977). Exploratory Data Analysis . Addison-Wesley.
- Benjamini, Y. (1988). "Opening the Box of a Boxplot". The American Statistician. 42 (4): 257–262. doi:10.2307/2685133. JSTOR 2685133.
- Rousseeuw, P. J.; Ruts, I.; Tukey, J. W. (1999). "The Bagplot: A Bivariate Boxplot". The American Statistician. 53 (4): 382–387. doi:10.2307/2686061. JSTOR 2686061.
Pranala luar
sunting- Kalkulator diagram kotak daring beserta penjelasan dan contoh
- Beeswarm Boxplot
- Pembuat diagram kotak daring yang kompleks dengan contoh data - lihat juga BoxPlotR: perkakas web untuk membuat diagram kotak Spitzer et al. Nature Methods 11, 121–122 (2014)