Pengguna:Kekavigi/bak pasir

Halaman ini berisi artikel tentang aljabar abstrak. Untuk hukum fisika, lihat Prinsip Archimedes.

Ilustrasi sifat Archimedes.

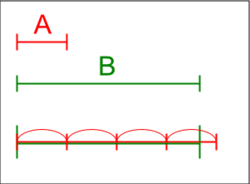
Dalam aljabar abstrak dan analisis, Sifat Archimedes, dinamai menurut ahli matematika Yunani kuno Archimedes dari Sirakusa, adalah sifat yang dimiliki oleh beberapa struktur aljabar, seperti grup, dan medan. Secara kasar, ini adalah sifat yang tidak memiliki elemen jauh lebih besar atau jauh lebih kecil . Adalah Otto Stolz yang memberi nama pada aksioma Archimedes karena muncul sebagai Aksioma V dari Archimedes Pada Bola dan Tabung .

Gagasan tersebut muncul dari teori besaran Yunani Kuno; itu masih memainkan peran penting dalam matematika modern seperti aksioma David Hilbert untuk geometri, dan teori grup terurut, medan terurut, dan medan lokal.

Struktur aljabar di mana dua elemen bukan nol adalah sebanding , dalam arti bahwa tidak satu pun dari mereka sangat kecil dibandingkan dengan yang lain, dikatakan Archimedes. Suatu struktur yang memiliki sepasang elemen bukan nol, yang salah satunya sangat kecil terhadap yang lain, dikatakan sebagai tak-Archimedes. Misalnya, grup terurut linear yang merupakan Archimedes adalah grup Archimedes.

Ini dapat dibuat tepat dalam berbagai konteks dengan rumusan yang sedikit berbeda.Misalnya, dalam konteks kolom terurut, satu memiliki aksioma Archimedes yang merumuskan sifat ini, di mana medan bilangan riil adalah Archimedes, tetapi fungsi rasional dalam koefisien riil tidak.

In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some algebraic structures, such as ordered or normed groups, and fields. The property, typically construed, states that given two positive numbers $x$ and $y$, there is an integer $n$ such that $nx>y$. It also means that the set of natural numbers is not bounded above. Roughly speaking, it is the property of having no infinitely large or infinitely small elements. It was Otto Stolz who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes’ On the Sphere and Cylinder.

The notion arose from the theory of magnitudes of Ancient Greece; it still plays an important role in modern mathematics such as David Hilbert's axioms for geometry, and the theories of ordered groups, ordered fields, and local fields.

An algebraic structure in which any two non-zero elements are comparable, in the sense that neither of them is infinitesimal with respect to the other, is said to be Archimedean. A structure which has a pair of non-zero elements, one of which is infinitesimal with respect to the other, is said to be non-Archimedean. For example, a linearly ordered group that is Archimedean is an Archimedean group.

This can be made precise in various contexts with slightly different formulations. For example, in the context of ordered fields, one has the axiom of Archimedes which formulates this property, where the field of real numbers is Archimedean, but that of rational functions in real coefficients is not.

Sejarah dan asal nama sifat Archimedes

Konsep ini dinamai oleh Otto Stolz (pada tahun 1880-an) setelah ahli geografi dan fisikawan Yunani kuno Archimedes dari Sirakusa.

Sifat Archimedes muncul di Buku V dari Elemen Euklides sebagai Definisi 4:

Besaran dikatakan memiliki rasio satu sama lain yang dapat, jika dikalikan, melebihi satu sama lain.

Karena Archimedes mengkreditkannya ke Eudoksos dari Knidos itu juga dikenal sebagai "Teorema Eudoxus" atau aksioma Eudoxus.

Archimedes menggunakan infinitesimal dalam argumen heuristik, meskipun ia menyangkal bahwa argumen tersebut telah selesai bukti matematika.

Definisi untuk grup terurut linear

Artikel utama: Grup Archimedean

Misalkanx dany menjadi elemen positif dari grup terurut linier G .

Kemudianx inifintesimal terhadap y (atau ekuivalen,y takhingga terhadapx) jika, untuk setiap bilangan asli n, kelipatan nx kurang dari y, yaitu, pertidaksamaan berikut berlaku:

${\underset {n{\text{ suku}}}{\underbrace {x+\dots +x} }}<y$

Definisi ini dapat diperluas ke seluruh kelompok dengan mengambil nilai mutlak.

Grup G adalah Archimedes jika tidak ada pasangan (x, y) sedemikian rupa sehingga x sangat kecil dibandingkan dengan y.

Selain itu, jika K adalah struktur aljabar dengan satuan (1) misalnya, gelanggang ,definisi serupa berlaku untuk K. Jika x sangat kecil dibandingkan dengan 1, maka x adalah elemen yang sangat kecil. Demikian juga, jikay tak hingga 1, maka y adalah elemen takhingga. Struktur aljabar K adalah Archimedes jika tidak memiliki elemen takhingga dan tidak memiliki elemen takhingga.

Medan terurut

Medan terurut memiliki beberapa sifat tambahan:

• Bilangan rasional adalah terbenam di setiap medan terurut. Artinya, setiap kolom terurut memiliki karakteristik nol.
• Jikax Infinitesimal, maka 1/x tidak terbatas, dan sebaliknya. Oleh karena itu, untuk memverifikasi bahwa medan adalah Archimedes, cukup dengan memeriksa hanya bahwa tidak ada elemen yang sangat kecil, atau untuk memeriksa bahwa tidak ada elemen yang tak terbatas.
• Jikax sangat kecil dan r adalah bilangan rasional, maka rx juga sangat kecil. Akibatnya, diberi elemen umum c, tiga bilangan c/2, c, dan 2c bisa jadi semua sangat kecil atau semua bukan sangat kecil.

Dalam setelan ini, medan terurutK adalah Archimedes persis ketika pernyataan berikut, disebut aksioma Archimedes, menyatakan:

"Misalkanx adalah elemen apa pun dari K. Kemudian ada bilangan asli n sehingga n > x."

Sebagai alternatif, seseorang dapat menggunakan karakterisasi berikut:

$\forall \,\varepsilon \in K{\big (}\varepsilon >0\implies \exists \ n\in N:1/n<\varepsilon {\big )}.$

Definisi untuk medan ternorma

Kualifikasi "Archimedes" juga diformulasikan dalam teori peringkat satu medan nilai dan ruang ternorma atas peringkat satu medan nilai sebagai berikut.

Misalkan F adalah medan yang diberkahi dengan fungsi nilai mutlak, yaitu fungsi yang mengaitkan bilangan real 0 dengan elemen medan 0 dan mengaitkan bilangan riil positif $|x|$ dengan setiap bukan nol x ∈ F dan dirumuskan

$|xy|=|x||y|$ dan $|x+y|\leq |x|+|y|$.

Kemudian, F dikatakan Archimedes jika ada bukan nol x ∈ F ada bilangan asli n dirumuskan

$|\underbrace {x+\cdots +x} _{n{\text{ terms}}}|>1.\,$

Demikian pula, ruang bernorma adalah Archimedes jika jumlah n suku, masing-masing sama dengan vektor bukan-nol x, memiliki norma yang lebih besar dari satu untuk cukup besar n.

medan dengan nilai mutlak atau ruang bernorma adalah Archimedes atau memenuhi ketentuan yang lebih kuat, yang disebut sebagai ultrametrik pertidaksamaan segitiga$|x+y|\leq \max(|x|,|y|)$,

masing-masing. medan atau ruang bernorma yang memenuhi pertidaksamaan segitiga ultrametrik disebut tak-Archimedes.

Konsep ruang linier bernorma tak-Archimedes diperkenalkan oleh A. F. Monna.

Lihat pula

• 0.999... – bilangan asli
• Ruang vektor berurutan Archimedean
• Konstruksi bilangan riil

Referensi

• Schechter, Eric (1997). Handbook of Analysis and its Foundations. Academic Press. ISBN 0-12-622760-8. Diarsipkan dari versi asli tanggal 2015-03-07. Diakses tanggal 2009-01-30. 

History and origin of the name of the Archimedean property

The concept was named by Otto Stolz (in the 1880s) after the ancient Greek geometer and physicist Archimedes of Syracuse.

The Archimedean property appears in Book V of Euclid's Elements as Definition 4:

Magnitudes are said to have a ratio to one another which can, when multiplied, exceed one another.

Because Archimedes credited it to Eudoxus of Cnidus it is also known as the "Theorem of Eudoxus" or the Eudoxus axiom.

Archimedes used infinitesimals in heuristic arguments, although he denied that those were finished mathematical proofs.

Definition for linearly ordered groups

Artikel utama: Archimedean group

Let x and y be positive elements of a linearly ordered group G. Then $x$ is infinitesimal with respect to $y$ (or equivalently, $y$ is infinite with respect to $x$) if, for any natural number $n$, the multiple $nx$ is less than $y$, that is, the following inequality holds:$$\underbrace {x+\cdots +x} _{n{\text{ terms}}}<y.\,$$This definition can be extended to the entire group by taking absolute values.

The group $G$ is Archimedean if there is no pair $(x,y)$ such that $x$ is infinitesimal with respect to $y$.

Additionally, if $K$ is an algebraic structure with a unit (1) — for example, a ring — a similar definition applies to $K$. If $x$ is infinitesimal with respect to $1$, then $x$ is an infinitesimal element. Likewise, if $y$ is infinite with respect to $1$, then $y$ is an infinite element. The algebraic structure $K$ is Archimedean if it has no infinite elements and no infinitesimal elements.

Ordered fields

Ordered fields have some additional properties:

• The rational numbers are embedded in any ordered field. That is, any ordered field has characteristic zero.
• If $x$ is infinitesimal, then $1/x$ is infinite, and vice versa. Therefore, to verify that a field is Archimedean it is enough to check only that there are no infinitesimal elements, or to check that there are no infinite elements.
• If $x$ is infinitesimal and $r$ is a rational number, then $rx$ is also infinitesimal. As a result, given a general element $c$, the three numbers $c/2$, $c$, and $2c$ are either all infinitesimal or all non-infinitesimal.

In this setting, an ordered field K is Archimedean precisely when the following statement, called the axiom of Archimedes, holds:

"Let $x$ be any element of $K$. Then there exists a natural number $n$ such that $n>x$."

Alternatively one can use the following characterization:$$\forall \,\varepsilon \in K{\big (}\varepsilon >0\implies \exists \ n\in N:1/n<\varepsilon {\big )}.$$

Definition for normed fields

The qualifier "Archimedean" is also formulated in the theory of rank one valued fields and normed spaces over rank one valued fields as follows. Let $K$ be a field endowed with an absolute value function, i.e., a function which associates the real number $0$ with the field element 0 and associates a positive real number $|x|$ with each non-zero $x\in K$ and satisfies $|xy|=|x||y|$ and $|x+y|\leq |x|+|y|$. Then, $K$ is said to be Archimedean if for any non-zero $x\in K$ there exists a natural number $n$ such that$$|\underbrace {x+\cdots +x} _{n{\text{ terms}}}|>1.$$Similarly, a normed space is Archimedean if a sum of $n$ terms, each equal to a non-zero vector $x$, has norm greater than one for sufficiently large $n$. A field with an absolute value or a normed space is either Archimedean or satisfies the stronger condition, referred to as the ultrametric triangle inequality,$$|x+y|\leq \max(|x|,|y|),$$respectively. A field or normed space satisfying the ultrametric triangle inequality is called non-Archimedean.

The concept of a non-Archimedean normed linear space was introduced by A. F. Monna.

Examples and non-examples

Archimedean property of the real numbers

The field of the rational numbers can be assigned one of a number of absolute value functions, including the trivial function $|x|=1$, when $x\neq 0$, the more usual ${\textstyle |x|={\sqrt {x^{2}}}}$, and the $p$-adic absolute value functions. By Ostrowski's theorem, every non-trivial absolute value on the rational numbers is equivalent to either the usual absolute value or some $p$-adic absolute value. The rational field is not complete with respect to non-trivial absolute values; with respect to the trivial absolute value, the rational field is a discrete topological space, so complete. The completion with respect to the usual absolute value (from the order) is the field of real numbers. By this construction the field of real numbers is Archimedean both as an ordered field and as a normed field. On the other hand, the completions with respect to the other non-trivial absolute values give the fields of p-adic numbers, where $p$ is a prime integer number (see below); since the $p$-adic absolute values satisfy the ultrametric property, then the $p$-adic number fields are non-Archimedean as normed fields (they cannot be made into ordered fields).In the axiomatic theory of real numbers, the non-existence of nonzero infinitesimal real numbers is implied by the least upper bound property as follows. Denote by $Z$ the set consisting of all positive infinitesimals. This set is bounded above by $1$. Now assume for a contradiction that $Z$ is nonempty. Then it has a least upper bound $c$, which is also positive, so $c/2<c<2c$. Since c is an upper bound of $Z$ and $2c$ is strictly larger than $c$, $2c$ is not a positive infinitesimal. That is, there is some natural number $n$ for which $1/n<2c$. On the other hand, $c/2$ is a positive infinitesimal, since by the definition of least upper bound there must be an infinitesimal $x$ between $c/2$ and $c$, and if $1/k<c/2\leq x$ then $x$ is not infinitesimal. But $1/(4n)<c/2$, so $c/2$ is not infinitesimal, and this is a contradiction. This means that $Z$ is empty after all: there are no positive, infinitesimal real numbers.

The Archimedean property of real numbers holds also in constructive analysis, even though the least upper bound property may fail in that context.

Non-Archimedean ordered field

Artikel utama: Non-Archimedean ordered field

For an example of an ordered field that is not Archimedean, take the field of rational functions with real coefficients. (A rational function is any function that can be expressed as one polynomial divided by another polynomial; we will assume in what follows that this has been done in such a way that the leading coefficient of the denominator is positive.) To make this an ordered field, one must assign an ordering compatible with the addition and multiplication operations. Now $f>g$ if and only if $f-g>0$, so we only have to say which rational functions are considered positive. Call the function positive if the leading coefficient of the numerator is positive. (One must check that this ordering is well defined and compatible with addition and multiplication.) By this definition, the rational function $1/x$ is positive but less than the rational function $1$. In fact, if $n$ is any natural number, then $n(1/x)=n/x$ is positive but still less than $1$, no matter how big $n$ is. Therefore, $1/x$ is an infinitesimal in this field.

This example generalizes to other coefficients. Taking rational functions with rational instead of real coefficients produces a countable non-Archimedean ordered field. Taking the coefficients to be the rational functions in a different variable, say $y$, produces an example with a different order type.

Non-Archimedean valued fields

The field of the rational numbers endowed with the p-adic metric and the p-adic number fields which are the completions, do not have the Archimedean property as fields with absolute values. All Archimedean valued fields are isometrically isomorphic to a subfield of the complex numbers with a power of the usual absolute value.

Equivalent definitions of Archimedean ordered field

Every linearly ordered field $K$ contains (an isomorphic copy of) the rationals as an ordered subfield, namely the subfield generated by the multiplicative unit $1$ of $K$, which in turn contains the integers as an ordered subgroup, which contains the natural numbers as an ordered monoid. The embedding of the rationals then gives a way of speaking about the rationals, integers, and natural numbers in $K$. The following are equivalent characterizations of Archimedean fields in terms of these substructures.

1. The natural numbers are cofinal in $K$. That is, every element of $K$ is less than some natural number. (This is not the case when there exist infinite elements.) Thus an Archimedean field is one whose natural numbers grow without bound.
2. Zero is the infimum in $K$ of the set $\{1/2,1/3,1/4,\dots \}$. (If $K$ contained a positive infinitesimal it would be a lower bound for the set whence zero would not be the greatest lower bound.)
3. The set of elements of $K$ between the positive and negative rationals is non-open. This is because the set consists of all the infinitesimals, which is just the set $\{0\}$ when there are no nonzero infinitesimals, and otherwise is open, there being neither a least nor greatest nonzero infinitesimal. Observe that in both cases, the set of infinitesimals is closed. In the latter case, (i) every infinitesimal is less than every positive rational, (ii) there is neither a greatest infinitesimal nor a least positive rational, and (iii) there is nothing else in between. Consequently, any non-Archimedean ordered field is both incomplete and disconnected.
4. For any $x$ in $K$ the set of integers greater than $x$ has a least element. (If $x$ were a negative infinite quantity every integer would be greater than it.)
5. Every nonempty open interval of $K$ contains a rational. (If $x$ is a positive infinitesimal, the open interval $(x,2x)$ contains infinitely many infinitesimals but not a single rational.)
6. The rationals are dense in $K$ with respect to both sup and inf. (That is, every element of $K$ is the sup of some set of rationals, and the inf of some other set of rationals.) Thus an Archimedean field is any dense ordered extension of the rationals, in the sense of any ordered field that densely embeds its rational elements.

See also

• 0.999... – bilangan asli
• Archimedean ordered vector space
• Construction of the real numbers

References

• Schechter, Eric (1997). Handbook of Analysis and its Foundations. Academic Press. ISBN 0-12-622760-8. Diarsipkan dari versi asli tanggal 2015-03-07. Diakses tanggal 2009-01-30. 

---

---

Dalam aljabar, kernel dari homomorfisme (fungsi yang mempertahankan struktur) umumnya gambar invers dari 0 (kecuali untuk grup yang operasinya dilambangkan dengan multi, dimana kernel adalah kebalikan dari gambar 1). Kasus khusus yang penting adalah kernel dari peta linear. kernel dari matriks, juga disebut ruang nol, adalah kernel dari peta linear yang ditentukan oleh matriks.

Kernel homomorfisme direduksi menjadi 0 (atau 1) jika dan hanya jika homomorfisme tersebut adalah injeksi, Artinya jika gambar invers dari setiap elemen terdiri dari satu elemen. Ini berarti bahwa kernel dapat dilihat sebagai ukuran sejauh mana homomorfisme gagal untuk diinjeksi.

Untuk beberapa jenis struktur, seperti grup abelian dan ruang vektor, kemungkinan kernel adalah substruktur dari jenis yang sama. Ini tidak selalu terjadi, dan terkadang, kemungkinan kernel telah menerima nama khusus, seperti subgrup normal untuk kelompok dan ideal dua sisi untuk cincin.

Kernel memungkinkan untuk menentukan objek hasil bagi (juga disebut aljabar hasil bagi di aljabar universal, dan kokernel di teori kategori). Untuk banyak jenis struktur aljabar, teorema fundamental homomorfisme (atau teorema isomorfisme pertama) menyatakan bahwa galeri dari homomorfisme adalah isomorfik terhadap hasil bagi oleh kernel.

Konsep kernel telah diperluas ke struktur sedemikian rupa sehingga gambar kebalikan dari satu elemen tidak cukup untuk memutuskan apakah homomorfisme adalah injeksi. Dalam kasus ini, kernel adalah hubungan kesesuaian.

Artikel ini adalah survei untuk beberapa jenis kernel penting dalam struktur aljabar.

Linear maps

Artikel utama: Kernel (aljabar linear)

Misalkan V dan W menjadi ruang vektor di atas bidang (atau lebih umum, modul di atas gelanggang dan biarkan T menjadi peta liear dari V ke W. Jika 0_W adalah vektor nol dari W , maka kernel T adalah preimage dari nol subruang {0_W}; that adalah, himpunan bagian dari V yang terdiri dari semua elemen V yang dipetakan oleh T ke elemen 0_W. Kernel biasanya dilambangkan sebagai ker T , atau variasinya:

$\operatorname {ker} T=\{\mathbf {v} \in V:T(\mathbf {v} )=\mathbf {0} _{W}\}{\text{.}}$

Karena peta linier mempertahankan vektor nol, vektor nol 0_V dari V harus menjadi milik kernel. Transformasi T bersifat injeksi jika dan hanya jika kernelnya direduksi menjadi subruang nol.

Kernel ker T selalu merupakan subruang linier dari V . Jadi, masuk akal untuk membicarakan tentang ruang hasil bagi V/(ker T). Teorema isomorfisme pertama untuk ruang vektor menyatakan bahwa ruang hasil bagi ini adalah isomorfis alami ke citra dari T (yang merupakan subruang dari W ). Akibatnya, dimensi dari V sama dengan dimensi kernel ditambah dimensi bayangan.

Jika V dan W adalah dimensi-hingga dan basis telah dipilih, maka T dapat dijelaskan oleh matriks M, dan kernel dapat dihitung dengan menyelesaikan sistem persamaan linear homogen Mv = 0. Dalam hal ini, kernel T dapat diidentifikasi ke kernel matriks M , juga disebut "spasi nol" dari M . Dimensi ruang kosong, disebut nulitas M , diberikan oleh jumlah kolom M dikurangi rank dari M , sebagai konsekuensi dari teori peringkat-nullity.

Memecahkan persamaan diferensial homogen sering kali sama dengan menghitung kernel operator diferensial tertentu. Misalnya, untuk mencari semua dua kali - fungsi terdiferensiasi s f dari garis nyata ke dirinya sendiri sehingga

$xf''(x)+3f'(x)=f(x),$

biarkan V menjadi ruang dari semua fungsi yang dapat dibedakan dua kali, biarkan W menjadi ruang dari semua fungsi, dan tentukan operator linier T dari V menjadi W oleh

$(Tf)(x)=xf''(x)+3f'(x)-f(x)$

untuk f di V dan x sembarang bilangan real. Maka semua solusi persamaan diferensial ada di ker T .

Seseorang dapat mendefinisikan kernel untuk homomorfisme antara modul melalui gelanggang dengan cara yang analog. Ini termasuk kernel untuk homomorfisme antara grup abelian sebagai kasus khusus. Contoh ini menangkap esensi kernel secara umum kategori abelian; lihat Kernel (teori kategori).

Aljabar dengan struktur nonaljabar

Kadang-kadang aljabar dilengkapi dengan struktur nonaljabar di samping operasi aljabar mereka. Misalnya, seseorang dapat mempertimbangkan grup topologi atau ruang vektor topologis, dengan dilengkapi dengan topologi. Dalam hal ini, kita mengharapkan homomorfisme f untuk mempertahankan struktur tambahan ini; dalam contoh topologi, kita ingin f menjadi peta kontinu. Prosesnya mungkin mengalami hambatan dengan aljabar hasil bagi, yang mungkin tidak berperilaku baik. Dalam contoh topologi, kita dapat menghindari masalah dengan mensyaratkan bahwa struktur aljabar topologi menjadi Hausdorff (seperti yang biasanya dilakukan); maka kernel (bagaimanapun itu dibangun) akan menjadi set tertutup dan ruang hasil bagi akan berfungsi dengan baik (dan juga Hausdorff).

Kernel dalam teori kategori

Pengertian kernel dalam teori kategori adalah generalisasi dari kernel abelian aljabar; lihat Kernel (teori kategori). Generalisasi kategorikal dari kernel sebagai hubungan kesesuaian adalah pasangan kernel . (Ada juga pengertian kernel perbedaan, atau biner equalizer.)

Lihat pula

• Kernel (aljabar linear)
• Himpunan nol

Referensi

• Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra (edisi ke-3rd). Wiley. ISBN 0-471-43334-9. 

• Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. Springer. ISBN 0-387-95385-X. 

---

In algebra, the kernel of a homomorphism (function that preserves the structure) is generally the inverse image of 0 (except for groups whose operation is denoted multiplicatively, where the kernel is the inverse image of 1). An important special case is the kernel of a linear map. The kernel of a matrix, also called the null space, is the kernel of the linear map defined by the matrix.

The kernel of a homomorphism is reduced to 0 (or 1) if and only if the homomorphism is injective, that is if the inverse image of every element consists of a single element. This means that the kernel can be viewed as a measure of the degree to which the homomorphism fails to be injective.

For some types of structure, such as abelian groups and vector spaces, the possible kernels are exactly the substructures of the same type. This is not always the case, and, sometimes, the possible kernels have received a special name, such as normal subgroup for groups and two-sided ideals for rings.

Kernels allow defining quotient objects (also called quotient algebras in universal algebra, and cokernels in category theory). For many types of algebraic structure, the fundamental theorem on homomorphisms (or first isomorphism theorem) states that image of a homomorphism is isomorphic to the quotient by the kernel.

The concept of a kernel has been extended to structures such that the inverse image of a single element is not sufficient for deciding whether a homomorphism is injective. In these cases, the kernel is a congruence relation.

This article is a survey for some important types of kernels in algebraic structures.

Survey of examples

Linear maps

Artikel utama: Kernel (linear algebra)

Let V and W be vector spaces over a field (or more generally, modules over a ring) and let T be a linear map from V to W. If 0_W is the zero vector of W, then the kernel of T is the preimage of the zero subspace {0_W}; that is, the subset of V consisting of all those elements of V that are mapped by T to the element 0_W. The kernel is usually denoted as ker T, or some variation thereof:

$\ker T=\{\mathbf {v} \in V:T(\mathbf {v} )=\mathbf {0} _{W}\}.$

Since a linear map preserves zero vectors, the zero vector 0_V of V must belong to the kernel. The transformation T is injective if and only if its kernel is reduced to the zero subspace.

The kernel ker T is always a linear subspace of V. Thus, it makes sense to speak of the quotient space V / (ker T). The first isomorphism theorem for vector spaces states that this quotient space is naturally isomorphic to the image of T (which is a subspace of W). As a consequence, the dimension of V equals the dimension of the kernel plus the dimension of the image.

If V and W are finite-dimensional and bases have been chosen, then T can be described by a matrix M, and the kernel can be computed by solving the homogeneous system of linear equations Mv = 0. In this case, the kernel of T may be identified to the kernel of the matrix M, also called "null space" of M. The dimension of the null space, called the nullity of M, is given by the number of columns of M minus the rank of M, as a consequence of the rank–nullity theorem.

Solving homogeneous differential equations often amounts to computing the kernel of certain differential operators. For instance, in order to find all twice-differentiable functions f from the real line to itself such that

$xf''(x)+3f'(x)=f(x),$

let V be the space of all twice differentiable functions, let W be the space of all functions, and define a linear operator T from V to W by

$(Tf)(x)=xf''(x)+3f'(x)-f(x)$

for f in V and x an arbitrary real number. Then all solutions to the differential equation are in ker T.

One can define kernels for homomorphisms between modules over a ring in an analogous manner. This includes kernels for homomorphisms between abelian groups as a special case. This example captures the essence of kernels in general abelian categories; see Kernel (category theory).

Group homomorphisms

Let G and H be groups and let f be a group homomorphism from G to H. If e_H is the identity element of H, then the kernel of f is the preimage of the singleton set {e_H}; that is, the subset of G consisting of all those elements of G that are mapped by f to the element e_H.

The kernel is usually denoted ker f (or a variation). In symbols:

$\ker f=\{g\in G:f(g)=e_{H}\}.$

Since a group homomorphism preserves identity elements, the identity element e_G of G must belong to the kernel.

The homomorphism f is injective if and only if its kernel is only the singleton set {e_G}. If f were not injective, then the non-injective elements can form a distinct element of its kernel: there would exist a, b ∈ G such that a ≠ b and f(a) = f(b). Thus f(a)f(b)⁻¹ = e_H. f is a group homomorphism, so inverses and group operations are preserved, giving f(ab⁻¹) = e_H; in other words, ab⁻¹ ∈ ker f, and ker f would not be the singleton. Conversely, distinct elements of the kernel violate injectivity directly: if there would exist an element g ≠ e_G ∈ ker f, then f(g) = f(e_G) = e_H, thus f would not be injective.

ker f is a subgroup of G and further it is a normal subgroup. Thus, there is a corresponding quotient group G / (ker f). This is isomorphic to f(G), the image of G under f (which is a subgroup of H also), by the first isomorphism theorem for groups.

In the special case of abelian groups, there is no deviation from the previous section.

Example

Let G be the cyclic group on 6 elements (0, 1, 2, 3, 4, 5} with modular addition, H be the cyclic on 2 elements (0, 1} with modular addition, and f the homomorphism that maps each element g in G to the element g modulo 2 in H. Then ker f = {0, 2, 4}, since all these elements are mapped to 0_H. The quotient group G / (ker f) has two elements: (0, 2, 4} and (1, 3, 5}. It is indeed isomorphic to H.

Ring homomorphisms

Let R and S be rings (assumed unital) and let f be a ring homomorphism from R to S. If 0_S is the zero element of S, then the kernel of f is its kernel as linear map over the integers, or, equivalently, as additive groups. It is the preimage of the zero ideal (0_S}, which is, the subset of R consisting of all those elements of R that are mapped by f to the element 0_S. The kernel is usually denoted ker f (or a variation). In symbols:

$\operatorname {ker} f=\{r\in R:f(r)=0_{S}\}.$

Since a ring homomorphism preserves zero elements, the zero element 0_R of R must belong to the kernel. The homomorphism f is injective if and only if its kernel is only the singleton set (0_R}. This is always the case if R is a field, and S is not the zero ring.

Since ker f contains the multiplicative identity only when S is the zero ring, it turns out that the kernel is generally not a subring of R. The kernel is a subrng, and, more precisely, a two-sided ideal of R. Thus, it makes sense to speak of the quotient ring R / (ker f). The first isomorphism theorem for rings states that this quotient ring is naturally isomorphic to the image of f (which is a subring of S). (Note that rings need not be unital for the kernel definition).

To some extent, this can be thought of as a special case of the situation for modules, since these are all bimodules over a ring R:

• R itself;
• any two-sided ideal of R (such as ker f);
• any quotient ring of R (such as R / (ker f)); and
• the codomain of any ring homomorphism whose domain is R (such as S, the codomain of f).

However, the isomorphism theorem gives a stronger result, because ring isomorphisms preserve multiplication while module isomorphisms (even between rings) in general do not.

This example captures the essence of kernels in general Mal'cev algebras.

Monoid homomorphisms

Let M and N be monoids and let f be a monoid homomorphism from M to N. Then the kernel of f is the subset of the direct product M × M consisting of all those ordered pairs of elements of M whose components are both mapped by f to the same element in N. The kernel is usually denoted ker f (or a variation thereof). In symbols:

$\operatorname {ker} f=\left\{\left(m,m'\right)\in M\times M:f(m)=f\left(m'\right)\right\}.$

Since f is a function, the elements of the form (m, m) must belong to the kernel. The homomorphism f is injective if and only if its kernel is only the diagonal set ((m, m) : m in M}.

It turns out that ker f is an equivalence relation on M, and in fact a congruence relation. Thus, it makes sense to speak of the quotient monoid M / (ker f). The first isomorphism theorem for monoids states that this quotient monoid is naturally isomorphic to the image of f (which is a submonoid of N; for the congruence relation).

This is very different in flavour from the above examples. In particular, the preimage of the identity element of N is not enough to determine the kernel of f.

Universal algebra

All the above cases may be unified and generalized in universal algebra.

General case

Let A and B be algebraic structures of a given type and let f be a homomorphism of that type from A to B. Then the kernel of f is the subset of the direct product A × A consisting of all those ordered pairs of elements of A whose components are both mapped by f to the same element in B. The kernel is usually denoted ker f (or a variation). In symbols:

$\operatorname {ker} f=\left\{\left(a,a'\right)\in A\times A:f(a)=f\left(a'\right)\right\}{\mbox{.}}$

Since f is a function, the elements of the form (a, a) must belong to the kernel.

The homomorphism f is injective if and only if its kernel is exactly the diagonal set ((a, a) : a ∈ A}.

It is easy to see that ker f is an equivalence relation on A, and in fact a congruence relation. Thus, it makes sense to speak of the quotient algebra A / (ker f). The first isomorphism theorem in general universal algebra states that this quotient algebra is naturally isomorphic to the image of f (which is a subalgebra of B).

Note that the definition of kernel here (as in the monoid example) doesn't depend on the algebraic structure; it is a purely set-theoretic concept. For more on this general concept, outside of abstract algebra, see kernel of a function.

Algebras with nonalgebraic structure

Sometimes algebras are equipped with a nonalgebraic structure in addition to their algebraic operations. For example, one may consider topological groups or topological vector spaces, which are equipped with a topology. In this case, we would expect the homomorphism f to preserve this additional structure; in the topological examples, we would want f to be a continuous map. The process may run into a snag with the quotient algebras, which may not be well-behaved. In the topological examples, we can avoid problems by requiring that topological algebraic structures be Hausdorff (as is usually done); then the kernel (however it is constructed) will be a closed set and the quotient space will work fine (and also be Hausdorff).

Kernels in category theory

The notion of kernel in category theory is a generalisation of the kernels of abelian algebras; see Kernel (category theory). The categorical generalisation of the kernel as a congruence relation is the kernel pair. (There is also the notion of difference kernel, or binary equaliser.)

See also

• Kernel (linear algebra)
• Zero set

References

• Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra (edisi ke-3rd). Wiley. ISBN 0-471-43334-9. 
• Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. Springer. ISBN 0-387-95385-X.