Peta Dymaxion

Peta Dymaxion atau Peta Fuller adalah proyeksi dari sebuah peta dunia dalam bentuk ikosahedron, which can be unfolded and flattened to two dimensions. The flat map is heavily interrupted in order to preserve shapes and sizes.

Peta Dymaxion yang belum dilipat.

The world on a Dymaxion projection, with 15° graticule

The Dymaxion projection with Tissot's indicatrix of deformation.

The world is flattened into a Dymaxion map as it unfolds into an icosahedron net with nearly contiguous land masses

This icosahedral net shows connected oceans surrounding Antarctica

An icosahedron, the shape the world map is projected onto before unfolding

Example of use illustrating early human migrations according to mitochondrial population genetics (numbers are millennia before present)

Dymaxion map of the world with the 30 largest countries and territories by total area, roughly to scale

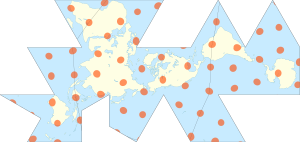
The projection was invented by Buckminster Fuller. The March 1, 1943 edition of Life magazine included a photographic essay titled "Life Presents R. Buckminster Fuller's Dymaxion World". The article included several examples of its use together with a pull-out section that could be assembled as a "three-dimensional approximation of a globe or laid out as a flat map, with which the world may be fitted together and rearranged to illuminate special aspects of its geography." Fuller applied for a patent in the United States in February 1944, the patent application showing a projection onto a cuboctahedron. The patent was issued in January 1946.

The 1954 version published by Fuller, made with co-cartographer Shoji Sadao, the Airocean World Map, used a modified but mostly regular icosahedron as the base for the projection, which is the version most commonly referred to today. This version depicts the Earth's continents as "one island", or nearly contiguous land masses.

The Dymaxion projection is intended only for representations of the entire globe. It is not a gnomonic projection, whereby global data expands from the center point of a tangent facet outward to the edges. Instead, each triangle edge of the Dymaxion map matches the scale of a partial great circle on a corresponding globe, and other points within each facet shrink toward its middle, rather than enlarging to the peripheries. Fuller's 1980 version of the Dymaxion map was the first definition and use of a mathematical transformation process to make the map. It is a polyhedral map projection.

The name Dymaxion was applied by Fuller to several of his inventions.

Properti

Fuller claimed that his map had several advantages over other projections for world maps.

It has less distortion of relative size of areas, most notably when compared to the Mercator projection; and less distortion of shapes of areas, notably when compared to the Gall–Peters projection. Other compromise projections attempt a similar trade-off.

More unusually, the Dymaxion map does not have any "right way up". Fuller argued that in the universe there is no "up" and "down", or "north" and "south": only "in" and "out". Gravitational forces of the stars and planets created "in", meaning "towards the gravitational center", and "out", meaning "away from the gravitational center". He attributed the north-up-superior/south-down-inferior presentation of most other world maps to cultural bias.

Fuller intended the map to be unfolded in different ways to emphasize different aspects of the world. Peeling the triangular faces of the icosahedron apart in one way results in an icosahedral net that shows an almost contiguous land mass comprising all of Earth's continents – not groups of continents divided by oceans. Peeling the solid apart in a different way presents a view of the world dominated

Pranala luar

• Buckminster Fuller Institute
• Fuller Map homepage Diarsipkan 2008-05-16 di Wayback Machine.
• PDF explanation of the map Diarsipkan 2006-03-05 di Wayback Machine.
• Dymaxion Project Animation Diarsipkan 2016-12-18 di Wayback Machine.
  • animation Diarsipkan 2006-12-08 di Wayback Machine. - Flash format
• Fuller Projection
• Icosahedron and Fuller maps
• Table of examples and properties of all common projections
• Metamute's rendition of the Dymaxion map 2001 Diarsipkan 2011-07-17 di Wayback Machine.
• Buckminster Fuller Virtual Institute Diarsipkan 2003-06-02 di Wayback Machine.