Distribusi Asimetrik Laplace

Dalam teori probabilitas dan statistik, Distribusi asimetrik laplace (ALD) adalah sebuah sebaran probabilitas berkelanjutan yang merupakan sebuah penyederhanaan dari distribusi laplace. Seperti distribusi laplace yang terdiri dari dua eksponensial distribusi yang memiliki skala yang sama yaitu x = m, Laplace asimetris sendiri terdiri dari dua eksponensial distribusi yang tidak sama skalanya berhadapan dengan x = m, disesuaikan untuk menjamin kontinuitas dan normalisasi grafik. Perbedaan dari dua varietas yang didistribusikan secara exponensial dengan cara yang berbeda dan pembobotan parameter yang didistribusikan menurut ALD. Ketika dua tingkat parameter tersebut bernilai sama, perbedaan akan didistribusikan menurut distribusi Laplace.

Asimetrik Laplace

Fungsi kepekatan probabilitas 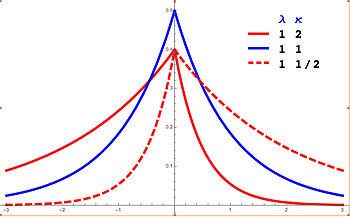PDF Asimetrik Laplace dengan m bernilai = 0. Perhatikan bahwa κ =  2 dan 1/2 dari kurva tersebut adalah duplikasi cerminan
Fungsi distribusi kumulatif 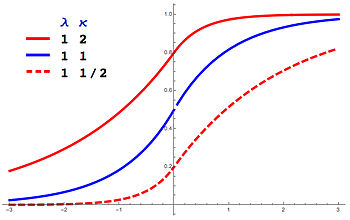CDF Asimetrik Laplace dengan m = 0.
Parameter	$m$ location (real) $\lambda >0$ scale (real) $\kappa >0$ asymmetry (real)
Dukungan	$x\in (-\infty ;+\infty )\,$
PDF	(see article)
CDF	(see article)
Mean	$m+{\frac {1-\kappa ^{2}}{\lambda \kappa }}$
Median	$m+(\kappa /\lambda )\log \left({\frac {1+\kappa ^{2}}{2\kappa ^{2}}}\right)$
Variance	${\frac {1+\kappa ^{4}}{\lambda ^{2}\kappa ^{2}}}$
Skewness	${\frac {2\left(1-\kappa ^{6}\right)}{\left(\kappa ^{4}+1\right)^{3/2}}}$
Entropi	$\log \left(e\,{\frac {1+\kappa ^{2}}{\kappa \lambda }}\right)$
CF	${\frac {e^{imt}}{(1+{\frac {it\kappa }{\lambda }})(1-{\frac {it}{\kappa \lambda }})}}$

Karakterisasi

Fungsi kepadatan probabilitas

Sebuah variabel acak memiliki sebuah distribusi asimetris Laplace(m, λ, κ) jika fungsi kepadatan probabilitas adalah

$f(x;m,\lambda ,\kappa )=\left({\frac {\lambda }{\kappa +1/\kappa }}\right)\,e^{-(x-m)\lambda \,s\kappa ^{s}}$

di mana s=sgn(x-m), atau:

$f(x;m,\lambda ,\kappa )={\frac {\lambda }{\kappa +1/\kappa }}{\begin{cases}\exp \left((\lambda /\kappa )(x-m)\right)&{\text{if }}x<m\\[4pt]\exp(-\lambda \kappa (x-m))&{\text{if }}x\geq m\end{cases}}$

Di sini, m adalah parameter lokasi, λ > 0 adalah parameter skala, dan κ adalah asimetri parameter. Ketika κ = 1, (x-m)s κ^s menyederhanakan ke -x|m| dan distribusi tersebut disederhanakan ke distribusi Laplace.