Vektor null

Dalam matematika, diberikan sebuah ruang vektor $X$ dengan sebuah bentuk kuadrat berkait $q$, ditulis $(X,q)$, sebuah vektor null atau vektor isotropik adalah sebuah elemen $x$ bukan nol dari $X$ untuk $q(x)=0$.

Sebuah kerucut null dimana $q(x,y,z)=x^{2}+y^{2}-z^{2}.$

Dalam teori dari bentuk bilinear real, bentuk kuadrat tentu, dan bentuk kuadrat isotropik berbeda. Mereka dibedakan hanya untuk terakhir terdapat sebuah vektor null bukan nol.

Sebuah ruang kuadrat $(X,q)$ yang memiliki sebuah vektor null disebut ruang pseudo-Euklidean.

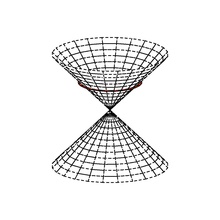
Sebuah ruang bektor pseudo-Euklidean mungkin menguraikan (bukan secara unik) menjadi subruang ortogonal $A$ dan $B$, $X=A+B$, dimana $q$ adalah positif-tentu pada $A$ dan negatif-tentu pada $B$. Kerucut null, atau kerucut isotropik, dari $X$ terdiri dari gabungan dari bola seimbangː

$\bigcup _{r\geq 0}\{x=a+b:q(a)=-q(b)=r,a\in A,b\in B\}.$

Kerucut null juga gabungan dari garis isotropik melalui asalnya.

Contoh

Vektor light-like dari ruang Minkowski adalah vektor null.

Empat kebebasan linear bikuaternion $l=1+hi$, $n=1+hj$, $m=1+hk$, dan $m^{*}=1-hk$ adalah vektor null dan $(l,n,m,m^{*})$ bisa berfungsi sebagai sebuah basis untuk subruang digunakan untuk mewakili ruang waktu. Vektor null juga digunakan dalam formalism Newman-Penrose mendekati ke manifold ruang waktu.

Sebuah aljabar komposisi terbagi ketika memiliki sebuah vektor null, jika tidak itu adalah aljabar pembagian.

Dalam modul Verma dari aljabar Lie terdapat vektor null.

Referensi

• Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. (1984). Modern Geometry: Methods and Applications. Diterjemahkan oleh Burns, Robert G. Springer. hlm. 50. ISBN 0-387-90872-2. 
• Shaw, Ronald (1982). Linear Algebra and Group Representations. 1. Academic Press. hlm. 151. ISBN 0-12-639201-3. 
• Neville, E. H. (Eric Harold) (1922). Prolegomena to Analytical Geometry in Anisotropic Euclidean Space of Three Dimensions. Cambridge University Press. hlm. 204.