Dimensi

"0d" beralih ke halaman ini. Untuk 0D, lihat 0d (disambiguasi).

Untuk kegunaan lain, lihat Dimensi (disambiguasi).

Dalam fisika dan matematika, dimensi dari suatu ruang atau objek secara informal diartikan sebagai jumlah minimal koordinat yang dibutuhkan untuk menentukan titik-titik yang ada di dalamnya. Jadi, sebuah garis memiliki dimensi karena hanya satu koordinat yang dibutuhkan untuk menentukan suatu titik di permukaannya (misalnya titik di garis angka 5). Permukaan seperti bidang atau permukaan suatu tabung atau sfer memiliki dimensi keduanya karena dibutuhkan dua koordinat untuk menentukan titik pada permukaannya (misalnya untuk menentukan titik di permukaan dibutuhkan lintang dan bujurnya). Bagian dalam kubus, tabung atau sfer bersifat tiga dimensi karena dibutuhkan tiga koordinat untuk menentukan suatu titik di dalam ruangnya.

Dari kiri ke kanan, persegi, kubus, dan teserak. Persegi dikelilingi oleh garis 1 dimensi, kubus oleh bidang 2 dimensi, dan teserak oleh volum 3 dimensi. Proyeksi kubus terjadi karena ditampilkan pada layar dua dimensi. Hal yang sama berlaku pada teserak, yang hanya bisa dilihat sebagai proyeksi bahkan dalam ruang tiga dimensi.

Diagram yang memperlihatkan empat dimensi ruang pertama.

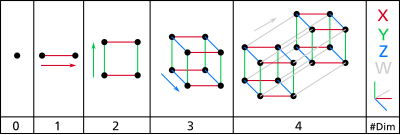
Dalam istilah fisika, dimensi merujuk pada struktur konstituen dari semua ruang (volum) dan posisinya dalam waktu (dipersepsikan sebagai dimensi skalar di sepanjang sumbu t), serta cakupan spasial objek-objek di dalamnya – struktur yang memiliki korelasi dengan konsep partikel dan medan yang berinteraksi sesuai relativitas massa dan pada dasarnya bersifat matematis. Sumbu ini atau sumbu lainnya dapat diarahkan untuk mengidentifikasi suatu titik atau struktur dalam tanggapan dan hubungannya terhadap objek lain. Teori fisika yang mencakup unsur waktu (misalnya relativitas umum) dianggap terjadi dalam "ruang waktu" empat dimensi yang didefinisikan sebagai ruang Minkowski). Teori modern cenderung lebih "berdimensi tinggi", termasuk teori medan kuantum dan string. Ruang tetap mekanika kuantum adalah ruang fungsi berdimensi tidak terbatas.

Konsep dimensi tidak dibatasi hingga benda fisik saja. Ruang berdimensi tinggi sering muncul dalam matematika dan ilmu pengetahuan atas berbagai alasan, terutama dalam bentuk ruang konfigurasi sebagaimana mekanika Lagrange atau Hamilton; keduanya adalah ruang abstrak dan terbebas dari ruang fisik yang di tempati manusia.

Lihat pula

• Tingkatan kebebasan
• Analisis dimensional
• Dimensi fraktal
• Hiperruang
• Dimensi intrinsik

Bacaan lanjutan

• Edwin A. Abbott, (1884) Flatland: A Romance of Many Dimensions, Public Domain. Online version with ASCII approximation of illustrations at Project Gutenberg.
• Thomas Banchoff, (1996) Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, Freeman.
• Clifford A. Pickover, (1999) Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press.
• Rudy Rucker, (1984) The Fourth Dimension, Houghton-Mifflin.
• Michio Kaku, (1994) Hyperspace, a Scientific Odyssey Through the 10th Dimension, Oxford University Press.