Fungsi hiperbolik invers

Dalam matematika, fungsi hiperbolik invers merupakan fungsi invers dari fungsi hiperbolik.

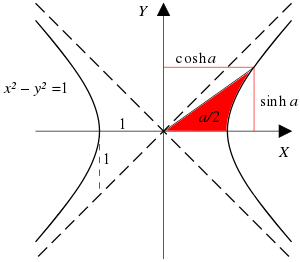
Sebuah sinar yang melalui grafik hiperbola satuan $x^{2}\ -\ y^{2}\ =\ 1$ di titik $(\cosh \,a,\,\sinh \,a)$, dengan $a$ bernilai dua kali lipat dari luas di antara sinar dengan grafik hiperbola dan sumbu-$x$.

Fungsi hiperbolik invers

Asal-usul prefiks ar- berasal dari singkatan dari notasi fungsi hiperbolik yang serupa (seperti, arsinh dan arcosh) berdasarkan ISO 80000-2. Prefiks arc- yang berasal dari fungsi hiperbolik yang serupa (seperti, arcsinh dan arccosh) juga seringkali dipakai berdasarkan penamaan fungsi invers trigonometri. Namun sayangnya, pemakaian kedua prefiks tersebut keliru sebab prefiks arc merupakan singkatan dari arcus, sedangkan prefiks ar merupakan singkatan dari area (bahasa Indonesia: luas, daerah). Karena itu, fungsi hiperbolik secara tidak langsung dikaitkan dengan busur.

Notasi seperti sinh⁻¹(x), cosh⁻¹(x), dst. juga dipakai sebagai penggantinya. Namun sayangnya, superskrip −1 membingungkan para pembaca karena dapat diartikan sebagai perpangkatan atau fungsi invers (sebagai contoh, bandingkan cosh⁻¹(x) dengan cosh(x)⁻¹).

Definisi fungsi invers hiperbolik dalam logaritma

Karena fungsi hiperbolik merupakan fungsi rasional dari e^x, dengan derajat pada pembilang maupun penyebut setidaknya bernilai dua, fungsi-fungsi tersebut dapat diselesaikan dalam bentuk e^x dengan menggunakan rumus kuadratik. Maka, dengan mengambil logaritma alami akan memberikan eksrespi berikut untuk fungsi hiperbolik invers.

Nama fungsi invers hiperbolik	Definisi fungsi invers hiperbolik dalam	Domain
Fungsi sinus hiperbolik invers:	$\operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)$	Di seluruh garis bilangan real
Fungsi kosinus hiperbolik invers	$\operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)$	Di interval tertutup [1, +∞ )
Fungsi tangen hiperbolik invers	$\operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)$	Di interval terbuka (−1, 1)
Fungsi kotangen hiperbolik invers	$\operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)$	Di gabungan dari interval terbuka (−∞, −1) dan (1, +∞)
Fungsi sekan hiperbolik invers	$\operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)$	Di interval semi- terbuka (0, 1]
Fungsi kosekan hiperbolik invers	$\operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)$	Di garis bilangan real, tetapi tidak memuat 0.

Rumus penambahan

$\operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)$

$\operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)$

$\operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)$

$\operatorname {arcoth} u\pm \operatorname {arcoth} v=\operatorname {arcoth} \left({\frac {1\pm uv}{u\pm v}}\right)$

${\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}$

Identitas lainnya

${\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ for }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ for }}x\geq 0\end{aligned}}$

$\ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)$

Komposisi dari fungsi hiperbolik dan fungsi hiperbolik invers

${\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{untuk}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{untuk}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{untuk}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{untuk}}\quad |x|>1\end{aligned}}$

Komposisi dari fungsi invers hiperbolik dan fungsi trigonometri

$\operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)$

$\ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)$

Konversi

$\ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)$

$\operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)$

$\operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)$

$\operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|$

Turunan

${\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ untuk semua bilangan real }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ untuk semua bilangan real }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ untuk semua bilangan real }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ untuk semua bilangan real }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ untuk semua bilangan real }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ untuk semua bilangan real }}x{\text{, kecuali }}0\\\end{aligned}}$

Sebagai contoh, misalkan $\theta =\operatorname {arsinh} x$, maka $${\frac {d\,\operatorname {arsinh} x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1+\sinh ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.$$dengan $\sinh ^{2}\theta =(\sinh \theta )^{2}$.

Ekspansi deret

Ekspansi deret dapat diperoleh untuk fungsi-fungsi di atas:

${\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

${\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}$

${\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

${\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

${\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}$

${\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

Ekspansi asimtotik untuk fungsi $\operatorname {arsinh} x$ dinyatakan dengan

$\operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}$

Bibilografi

• Herbert Busemann and Paul J. Kelly (1953) Projective Geometry and Projective Metrics, page 207, Academic Press.

Pranala luar

• Hazewinkel, Michiel, ed. (2001) [1994], "Inverse hyperbolic functions", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4