Ekuivalensi massa–energi

E = mc² dalam ilmu fisika adalah sebuah rumus yang paling dikenal bahkan beberapa orang yang tidak pandai fisika pun mengetahui nya dan persamaan tersebut sangat penting dalam menjelaskan persamaan nilai antara energi (E) dan massa (m), yang disetarakan secara langsung melalui konstanta kuadrat laju cahaya dalam vakum ( c ² )

E = mc² eksplanasi

Rumus Einstein th 1905 yang dipajang dengan ketinggian 4m di Berlin

$E=mc^{2}\!$,

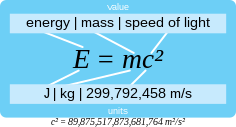
yang mana:

• E = energi (J)
• m = massa (kg)
• c = kecepatan cahaya (m.s^-1)

Faktor c ² bernilai 89.88 PJ/kg = 21.48 Mt TNT per kg = 149.3 pJ/u = 931.5 MeV/u.

Karena konsekuensi dari $c^{2}=a^{2}+b^{2}$ Maka persamaan ekuivalensi massa-energi bisa ditulis dengan $E=m(a^{2}+b^{2})$

Kebanyakan orang menggunakan satuan energi sebagai eV (electron volt)

dimaksud dalam persamaan di atas adalah energi diam, maka massa yang terkait adalah juga massa diam atau massa invarian.

${\begin{aligned}E_{r}^{2}-|{\vec {p}}\,|^{2}c^{2}&=m_{0}^{2}c^{4}\\E_{r}^{2}-(pc)^{2}&=(m_{0}c^{2})^{2}\end{aligned}}$

atau

$E_{r}={\sqrt {(m_{0}c^{2})^{2}+(pc)^{2}}}\,\!$

Sejarah dan konsekuensinya

Albert Einstein menurunkan rumus ini didasarkan atas pengamatannya pada tahun 1905 atas kelakuan objek yang bergerak dengan laju mendekati laju cahaya. Kesimpulan terkenal yang ditariknya dari pengamatan ini adalah bahwa massa sebuah benda sebenarnya adalah sebuah ukuran dari kandungan energi benda tersebut. Sebaliknya, persamaan yang dimaksud mengisyaratkan bahwa semua energi yang ada dalam sistem tertutup memengaruhi massa diam dari sistem.

$\mathrm {Energi} =\mathrm {Massa} \,\times \,(\mathrm {laju\ cahaya\ dalam\ vakum} )^{2}$

Menurut persamaan ini, jumlah maksimum energi yang "dapat diperoleh" dari suatu objek untuk melakukan kerja aktif adalah massa objek dikalikan kuadrat dari laju cahaya.

Rumus ini juga digunakan untuk mengukur besarnya energi yang dihasilkan dalam reaksi nuklir. Perubahan massa isotop sebelum dan sesudah reaksi nuklir diperhitungkan. Dimana jumlah massa yang hilang sesudah reaksi nuklir (Δm) dikalikan dengan kuadrat kecepatan cahaya, hasilnya sama dengan energi yang dilepaskan dalam reaksi nuklir tersebut.

$n_{0}^{1}+X_{N}^{A}\rightarrow Y_{N}^{B}+Energi(\Delta m)\!$

Lihat pula

• Reaksi nuklir
• Persamaan Klein-Gordon
• Fungsi gelombang relativistik

Referensi

• Bodanis, David (2001). E=mc²: A Biography of the World's Most Famous Equation. Berkley Trade. ISBN 0-425-18164-2. 
• Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman. ISBN 0-7167-4345-0. Pemeliharaan CS1: Banyak nama: authors list (link)

Pranala luar

• Stanford Encyclopedia of Philosophy entry
• Rekaman suara Einstein yang berisi penjelasan singkat tentang teori ini
• Penjelasan Rumus Einstein