Pengguna:Dedhert.Jr/Uji halaman 01.3

Jumlah luas dari dua persegi pada sisi $a$ dan $b$ sama dengan jumlah persegi pada hipotenusa $c$.

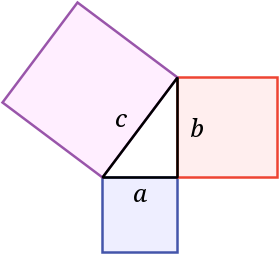
Dalam matematika, teorema Pythagoras adalah hubungan mendasar dalam geometri Euklides di antara tiga sisi segitiga siku-siku. Teorema ini mengatakan bahwa luas persegi pada hipotenusa segitiga sama dengan jumlah luas persegi pada dua sisi lainnya. Teorema ini dapat ditulis sebagai persamaan yang menghubungkan panjang sisi $a$, $b$, dan c, yang seringkali disebut persamaan Pythagoras:

$a^{2}+b^{2}=c^{2}$,

dimana c mewakili hipotenusa $a$ dan $b$ adalah panjang dari dua sisi segitiga lainnya. Teorema ini yang sejarahnya memiliki pokok perdebatan, dinamai dari ahli filsafat Yunani Pythagoras, yang lahir sekitar 570 SM.

Teorema Pythagoras telah dibuktikan berkali-kali melalui metode yang berbeda – mungkin paling banyak untuk setiap teorema matematika. Bukti teorema-teorema yang berasal dari ribuan tahun lalu ini bermacam-macam, di antaranya menggunakan bukti geometri dan aljabar.

Teorema Pythagoras dapat dirampat dalam berbagai cara, diantaranya untuk ruang berdimensi lebih tinggi, ruang yang bukan ruang Euklides, bangunan yang bukan segitiga siku-siku, dan bangunan yang bukan segitiga sama sekali namun berupa benda berdimensi-n. Teorema Pythagoras menarik minat di luar matematika sebagai simbol kemustahilan, mistik, atau kekuatan intelektual; referensi popular dalam sastra, drama, musik, lagu, perangko dan kartun berlimpah mengenai matematika.

Bentuk lain

Jika $c$ melambangkan panjang hipotenusa, dan $a$ dan $b$ melambangkan panjang dua sisi segitiga lainnya; teorema Pythagoras dapat dinyatakan sebagai persamaan Pythagoras:

$a^{2}+b^{2}=c^{2}$.

Jika panjang sisi $a$ dan $b$ diketahui, maka panjang hipotenusa $c$ dapat dihitung sebagai

$c={\sqrt {a^{2}+b^{2}}}$.

Jika panjang hipotenusa $c$ dan salah satu panjang sisi segitiga (yakni $a$ dan $b$) diketahui, maka panjang sisi lainnya dapat dihitung sebagai

$a={\sqrt {c^{2}-b^{2}}}$

atau

$b={\sqrt {c^{2}-a^{2}}}$.

Persamaan Pythagoras mengaitkan sisi-sisi pada segitiga siku-siku sehingga bila panjang kedua sisi segitiga diketahui, panjang sisi ketiga dapat ditemukan. Korolari teorema lainnya adalah bahwa hipotenusa untuk suatu segitiga siku-siku lebih besar dari sisi-sisi lainnya, tetapi lebih kecil dari jumlah sisi kuadrat.

Generalisasi teorema ini adalah hukum kosinus, yang menghitung panjang suatu sisi segitiga bila diketahui panjang dari dua sisi dan dua sudut pada segitiga. Jika sudut di antara dua sisi lainnya adalah sudut siku-siku, maka hukum kosinus disebut sebagai persamaan Pythagoras.

Bukti melalui persegi

Bukti penyusunan

Bukti penyusunan

Dalam bukti penyusunan, dua persegi yang memiliki panjang sisi $a+b$ dan memuat empat segitiga siku-siku dengan $a$ dan $b$ adalah panjang sisinya, dan $c$ adalah hipotenusa. Pada persegi yang pertama, segitiga diletakkan sehingga tepi persegi sesuai dengan sudut siku-siku pada segitiga, dan membentuk sebuah persegi di tengahnya dengan panjang sisinya adalah $c$. Masing-masing persegi mempunyai luas $(a+b)^{2}$ dan $2ab+c^{2}$, dengan $2ab$ mewakili total luas dari keempat segitiga. Pada persegi yang kedua, keempat segitiga dibentuk menjadi dua persegi panjang dengan panjang sisi $a$ dan $b$. Keempat segitiga tersebut diletakkan sehingga persegi dengan panjang sisi $a$ membentuk di tepi persegi, dan persegi dengan panjang sisi $b$ membentuk di tepi persegi lainnya. Persegi yang kedua akan mempunyai luas $(a+b)^{2}$ dan $2ab+a^{2}+b^{2}$. Karena kedua persegi mempunyai luas $(a+b)^{2}$, maka dapat dikatakan bahwa luas persegi juga sama dengan luas persegi lainnya sehingga $2ab+c^{2}$ = $2ab+a^{2}+b^{2}$. Dengan menghilangkan luas dari keempat persegi pada kedua ruas persamaan akan memberikan rumus $a^{2}+b^{2}=c^{2}.$

Dalam bukti lainnya, persegi panjang pada kotak kedua juga dapat diletakkan sehingga kedua persegi mempunyai sebuah tepi yang berpadanan dengan tepi persegi yang berurutan. Dalam hal ini juga dapat membentuk dua kotak, kali ini dalam bentuk persegi dengan tepi yang berurutan, dengan luas $a^{2}$ dan $b^{2}$. Hal ini lagi mengacu pada persegi kdeua dengan luasnya $2ab+a^{2}+b^{2}$.

Sir Thomas Heath, seorang matematikawan asal Inggris, memberikan bukti tersebut dalam komentarnya pada Proposisi I.47 dalam Euclid's Elements. Ia menyebutkan usulannya kepada matematikawan asal Jerman, Carl Anton Bretschneider dan Hermann Hankel, bahwa Pythagoras mungkin mengetahui bukti tersebut. Heath sendiri menyukai usulan yang berbeda mengenai bukti Pythagoras, tetapi Heath mengatakan permulaan diskusinya "bahwa kesusateraan Yunani yang kita miliki merupakan milik dari abad kelima pertama setelah Pythagoras tidak menyebutkan hal ini atau penemuan geometri besar lainnya kepadanya." Pengetahuan terbaru ini telah menimbulkan keraguan yang semakin besar pada segala jenis peran untuk Pythagoras sebagai pencipta matematika, meskipun perdebatan berlanjut.

Bukti melalui aljabar

Teorema Pythagoras dapat dibuktikan secara aljabar melalui empat salinan dari segitiga yang sama yang disusun secara simetris di sekitar persegi dengan sisi $c$, seperti yang diperlihatkan pada gambar sebelumnya. Hal ini menghasilkan sebuah persegi yang lebih besar, dengan sisi $a+b$ dan luas $(a+b)^{2}$. Keempat segitiga dan persegi dengan sisi c harus mempunyai luas yang sama dengan luas persegi yang lebih besar, yang dirumuskan sebagai

$(b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab.$

Dengan menyusun ekspresi, memberikan

$c^{2}=(b+a)^{2}-2ab=b^{2}+2ab+a^{2}-2ab=a^{2}+b^{2}.$

Ada bukti serupa yang menggunakan empat salinan dari segitiga siku-siku dengan sisi a, b dan c, yang disusun dalam sebuah persegi dengan sisi c seperti pada gambar sebelumnya. Keempat segitiga tersebut sebangun dengan luasnya masing-masing sama dengan ${\tfrac {1}{2}}ab$, sedangkan persegi yang kecil mempunyai sisi b − a dan luas (b − a)². Karena itu, luas persegi dirumuskan

$(b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=b^{2}-2ab+a^{2}+2ab=a^{2}+b^{2}.$

Namun hal ini merupakan sebuah persegi dengan sisi c dan luas c², jadi

$c^{2}=a^{2}+b^{2}.$

Bukti teorema Pythagoras lainnya

Teorema Pythagoras memiliki banyak bukti yang diketahui daripada teorema lainnya (seperti hukum reprositas kuadrat yang menyainginya berdasarkan jumlah bukti); buku The Pythagorean Proposition memiliki 370 bukti.

Bukti menggunakan segitiga sebangun

Bukti menggunakan segitiga yang sebangun.

Bukti ini berdasarkan kesebandingan sisi yang sesuai pada dua segitiga yang sebangun. Dalam artian, bahwa perbandingan dua sisi yang sesuai dari segtiga yang sebangun sama terlepas dari ukuran segitiga.

Misalkan ABC adalah segitiga siku-siku, dengan C adalah sudut siku-siku. seperti yang diperlihatkan pada gambar di samping. Tariklah tinggi segitiga dari titik C hingga ke titik H, dimana H adalah titik perpotongan garis AB. Titik H membagi panjang hipotenusa c menjadi dua, yaitu d dan e. Segitiga baru ACH sebangun dengan segitiga ABC, karena kedua segitiga memiliki sudut siku-siku (menurut definisi tinggi segitiga). Kedua segitiga tersebut berbagi sudut A, dalam artian bahwa ada sudut ketiga juga akan sama pada kedua segitiga, yang ditandai dengan θ seperti pada gambar di samping. Dengan alasan yang serupa, segitiga CBH juga sebangun dengan ABC. Bukti kesebangunan dari segitiga-segitiga memerlukan postulat segitiga: Jumlah sudut dalam segitiga sama dengan dua kali sudut siku-siku, dan postulat ini ekuivalen dengan postulat kesejajaran. Kesebangunan segitiga mengacu pada persamaan dari perbandingan sisi:

${\frac {BC}{AB}}={\frac {BH}{BC}}$ dan ${\frac {AC}{AH}}={\frac {AB}{AC}}$.

Hasil pertama pada persamaan di atas sama dengan kosinus sudut θ, sedangkan hasil kedua sama dengan sinus dari sudut θ. Kedua perbandingan tersebut dapat ditulis sebagai

$BC^{2}=AB\times BH$ dan $AC^{2}=AB\times AH$.

Dengan menjumlahkan kedua persamaan tersebut, akan menghasilkan persamaan

$BC^{2}+AC^{2}=(AB\times BH)+(AB\times AH)=AB(AH+BH)=AB^{2}$.

Setelah penyederhanaan, persamaan tersebut menyatakan teorema Pythagoras:

$BC^{2}+AC^{2}=AB^{2}$.

Peran bukti di atas dalam sejarah merupakan subjek yang memiliki banyak spekulasi. Pertanyaan mendasarnya adalah mengapa Euklides tidak menggunakan bukti tersebut, melainkan menemukan bukti lain. Salah satu dugaan adalah bahwa bukti melalui segitiga yang sebangun melibatkan teori kesebandingan, topik yang tidak membahas bukti tersebut hingga muncul Elements, dan teori kesebandingan tersebut membutuhkan pengembangan lebih lanjut pada masa itu.

Bukti Euklides

Bukti Elements Euklides

Secara garis besar, berikut adalah bagaimana bukti dalam Elements Euklides berasal. Persegi yang besar dibagi menjadi persegi panjang sebelah kiri dan kanan. Sebuah segitiga digambar sehingga memiliki luas persegi panjang di sebelah kiri. Lalu, sebuah segitiga lain digambar sehingga memiliki luas persegi panjang di sisi paling kiri. Kedua buah segitiga tersebut terbukti kongruen, dengan membuktikan bahwa persegi tersebut memiliki luas yang sama dengan persegi panjang sebelah kiri. Argumen ini diikuti oleh versi yang sama mengenai persegi panjang sebelah kanan dan persegi yang tersisa. Dengan menempatkan dua persegi panjang bersama-sama untuk membentuk persegi kembali pada sisi miring, maka luasnya sama dengan jumlah luas dari dua persegi lainnya. Bukti penjelasannya sebagai berikut:

Misalkan A, B, dan C adalah puncak segitiga siku-siku, dengan A adalah sudut siku-siku. Tarik garis suatu tegak lurus dari A ke sisi yang berhadapan dengan hipotenusa dalam persegi pada hipotenusa. Garis tersebut membagi persegi pada hipotenusa menjadi dua persegi panjang, masing-masing mempunyai luas yang sama seperti salah satu dari dua persegi pada kakinya.

Untuk bukti formalnya memerlukan empat lema dasar:

1. Jika pada dua buah segitiga terdapat sepasang sisi di segitiga pertama sama panjang dengan sepasang sisi bersesuaian di segitiga kedua, dan sudut yang diapit kedua pasang sisi tersebut sama besar, maka dua segitiga tersebut kongruen (sisi-sudut-sisi).
2. Luas dari segitiga sama dengan setengah dari luas suatu jajargenjang pada alas dan tinggi yang sama.
3. Luas dari persegi panjang sama dengan hasil kali dari sisi damping.
4. Luas dari persegi panjang sama dengan hasil kali dari dua sisi persegi panjang (diikuti dari lema 3).

Selanjutnya, setiap persegi di atas berkaitan dengan segitiga yang kongruen dengan segitiga lain yang berkaitan in turn to one of two rectangles making up the lower square.

Ilustrasi yang memuat garis baru.

Gambar yang memperlihatkan dua segitiga kongruen dari setengah luas persegi panjang BDLK dan persegi BAGF.

Berikut adalah buktinya:

1. Misalkan ACB adalah segitiga bersudutkan siku-siku dengan sudut CAB adalah siku-siku.
2. Pada setiap sisi BC, AB, dan CA, persegi CBDE, BAGF, dan ACIH digambar sesuai urutannya. Dalam Euclid Element, gambaran persegi ini memerlukan teorema dahulu dan juga bergantung pada postular sejajar.
3. Dari A, tariklah sebuah garis yang sejajar dengan BD dan CE. Garis tersebut tegak lurus dan memotong garis BC di K dan DE di L.
4. Hubungkan garis CF dan AD sehingga membentuk segitiga BCF dan BDA.
5. Sudut CAB dan BAG adalah siku-siku. Karena itu C, A, dan G kolinear.
6. Sudut CBD dan FBA adalah siku-siku. Karena itu sudut ABD sama dengan sudut FBC, karena kedua sudut merupakan jumlah dari sudut siku-siku dan sudut ABC.
7. Karena AB sama dengan FB, BD sama dengan BC dan sudut ABD sama dengan FBC, maka segitiga ABD harus kongruen dengan segitiga FBC.
8. Karena titik A, K, dan L adalah garis lurus yang sejajar dengan BD, maka persegi panjang BDLK sama dengan dua kali dari luas segitiga ABD, karena mereka membagi alas BD dan mempunyai tinggi segitiga BK yang sama, yakni sebuah garis normal ke alas segitiga yang menghubungkan garis sejajar BD dan AL. (lema 2)
9. Karena C kolinear dengan A dan G, dan garis CAG sejajar dengan FB, maka persegi BAGF harus dua kali dari luas segitiga FBC.
10. Oleh karena itu, persegi panjang BDLK harus mempunyai luas yang sama seperti persegi BAGF = AB².
11. Dengan menerapkan dari langkah 3 ke 10 untuk sisi lain pada gambar berikut, hal ini dapat diperlihatkan dengan cara yang serupa bahwa persegi panjang CKLE harus mempunyai luas yang sama seperti ACIH = AC².
12. Dengan menambahkan kedua hasil tersebut, AB² + AC² = BD × BK + KL × KC.
13. Karena BD = KL, maka BD × BK+ KL × KC = BD(BK + KC) = BD × BC.
14. Oleh karena CBDE adalah persegi, maka AB² + AC² = BC².

Bukti yang muncul dari Proposisi 47 dalam kitab Elements Euklides yang pertama, memperlihatkan bahwa luas persegi pada hipotenusa sama dengan jumlah dari luas dari dua persegi lainnya. Bukti ini cukup berbeda dari bukti melalui kesebangunan segitiga, yang diduga merupakan bukti yang dipakai oleh Pythagoras.

Bukti melalui pemisahan dan penyusunan ulang

Bukti lainnya adalah dengan menyusun ulang segitiga siku-siku seperti yang diperlihatkan pada animasi berikut. Sebuah persegi yang besar dibentuk dengan luas c², dari empat segitiga siku-siku identik dengan sisi a, b dan c, dimuat di sekitar persegi berpusat yang kecil. Maka kedua persegi panjang dibentuk dengan sisi a dan b dengan memindahkan segitiga-segitiga tersebut. Dengan menggabungkan persegi yang lebih kecil dari persegi panjang tersebut menghasilkan dua persegi dengan luas masing-masing a² dan b², yang harus mempunyai luas yang sama dengan luas persegi besar yang awal.

Diagram of the two algebraic proofs

The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called dissection. This shows the area of the large square equals that of the two smaller ones.

Sebuah animasi yang memperlihatkan bukti dengan menyusun ulang keempat buah segitiga siku-siku yang identik

Sebuah animasi yang memperlihatkan bukti lain dengan menyusun ulang

Bukti melalui penyusunan lebih lanjut

Bukti Einstein melalui pemisahan tanpa menyusun ulang

Right triangle on the hypotenuse dissected into two similar right triangles on the legs, according to Einstein's proof

Albert Einstein gave a proof by dissection in which the pieces do not need to be moved. Instead of using a square on the hypotenuse and two squares on the legs, one can use any other shape that includes the hypotenuse, and two similar shapes that each include one of two legs instead of the hypotenuse (see Similar figures on the three sides). In Einstein's proof, the shape that includes the hypotenuse is the right triangle itself. The dissection consists of dropping a perpendicular from the vertex of the right angle of the triangle to the hypotenuse, thus splitting the whole triangle into two parts. Those two parts have the same shape as the original right triangle, and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. Because the ratio of the area of a right triangle to the square of its hypotenuse is the same for similar triangles, the relationship between the areas of the three triangles holds for the squares of the sides of the large triangle as well.

Bukti aljabar

A related proof was published by future U.S. President James A. Garfield (then a U.S. Representative) (see diagram). Instead of a square it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is

${\frac {1}{2}}(b+a)^{2}.$

The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of ${\frac {1}{2}}$, which is removed by multiplying by two to give the result.

Bukti melalui diferensial

One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing calculus.

The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length y, the side AC of length x and the side AB of length a, as seen in the lower diagram part.

Diagram for differential proof

If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. These form two sides of a triangle, CDE, which (with E chosen so CE is perpendicular to the hypotenuse) is a right triangle approximately similar to ABC. Therefore, the ratios of their sides must be the same, that is:

${\frac {dy}{dx}}={\frac {x}{y}}.$

This can be rewritten as $y\,dy=x\,dx$ , which is a differential equation that can be solved by direct integration:

$\int y\,dy=\int x\,dx\,,$

giving

$y^{2}=x^{2}+C.$

The constant can be deduced from x = 0, y = a to give the equation

$y^{2}=x^{2}+a^{2}.$

This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of dx and dy.

Converse

The converse of the theorem is also true:

For any three positive numbers a, b, and c such that a² + b² = c², there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.

An alternative statement is:

For any triangle with sides a, b, c, if a² + b² = c², then the angle between a and b measures 90°.

This converse also appears in Euclid's Elements (Book I, Proposition 48):

"If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right."

It can be proven using the law of cosines or as follows:

Let ABC be a triangle with side lengths a, b, and c, with a² + b² = c². Construct a second triangle with sides of length a and b containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length c = √a² + b², the same as the hypotenuse of the first triangle. Since both triangles' sides are the same lengths a, b and c, the triangles are congruent and must have the same angles. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle.

The above proof of the converse makes use of the Pythagorean theorem itself. The converse can also be proven without assuming the Pythagorean theorem.

A corollary of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let c be chosen to be the longest of the three sides and a + b > c (otherwise there is no triangle according to the triangle inequality). The following statements apply:

• If a² + b² = c², then the triangle is right.
• If a² + b² > c², then the triangle is acute.
• If a² + b² < c², then the triangle is obtuse.

Edsger W. Dijkstra has stated this proposition about acute, right, and obtuse triangles in this language:

sgn(α + β − γ) = sgn(a² + b² − c²),

where α is the angle opposite to side a, β is the angle opposite to side b, γ is the angle opposite to side c, and sgn is the sign function.

Consequences and uses of the theorem

Pythagorean triples

Artikel utama: Pythagorean triple

A Pythagorean triple has three positive integers a, b, and c, such that a² + b² = c². In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths. Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).

A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1).

The following is a list of primitive Pythagorean triples with values less than 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Reciprocal Pythagorean theorem

Given a right triangle with sides $a,b,c$ and altitude $d$ (a line from the right angle and perpendicular to the hypotenuse $c$). The Pythagorean theorem has,

$a^{2}+b^{2}=c^{2}$

while the reciprocal Pythagorean theorem or the upside down Pythagorean theorem relates the two legs $a,b$ to the altitude $d$,

${\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{d^{2}}}$

The equation can be transformed to,

${\frac {1}{(xz)^{2}}}+{\frac {1}{(yz)^{2}}}={\frac {1}{(xy)^{2}}}$

where $x^{2}+y^{2}=z^{2}$ for any non-zero real $x,y,z$. If the $a,b,d$ are to be integers, the smallest solution $a>b>d$ is then

${\frac {1}{20^{2}}}+{\frac {1}{15^{2}}}={\frac {1}{12^{2}}}$

using the smallest Pythagorean triple $3,4,5$. The reciprocal Pythagorean theorem is a special case of the optic equation

${\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{r}}$

where the denominators are squares and also for a heptagonal triangle whose sides $p,q,r$ are square numbers.

Incommensurable lengths

The spiral of Theodorus: A construction for line segments with lengths whose ratios are the square root of a positive integer

One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras' theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.

The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer. Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras' theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as √2, √3, √5 . For more detail, see Quadratic irrational.

Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit. According to one legend, Hippasus of Metapontum (ca. 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable.

Complex numbers

The absolute value of a complex number z is the distance r from z to the origin

For any complex number

$z=x+iy,$

the absolute value or modulus is given by

$r=|z|={\sqrt {x^{2}+y^{2}}}.$

So the three quantities, r, x and y are related by the Pythagorean equation,

$r^{2}=x^{2}+y^{2}.$

Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.

This can be generalised to find the distance between two points, z₁ and z₂ say. The required distance is given by

$|z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}},$

so again they are related by a version of the Pythagorean equation,

$|z_{1}-z_{2}|^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}.$

Euclidean distance

Informasi lebih lanjut: Euclidean distance

The distance formula in Cartesian coordinates is derived from the Pythagorean theorem. If (x₁, y₁) and (x₂, y₂) are points in the plane, then the distance between them, also called the Euclidean distance, is given by

${\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.$

More generally, in Euclidean n-space, the Euclidean distance between two points, $A\,=\,(a_{1},a_{2},\dots ,a_{n})$ and $B\,=\,(b_{1},b_{2},\dots ,b_{n})$, is defined, by generalization of the Pythagorean theorem, as:

${\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}}}={\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.$

If instead of Euclidean distance, the square of this value (the squared Euclidean distance, or SED) is used, the resulting equation avoids square roots and is simply a sum of the SED of the coordinates:

$(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}=\sum _{i=1}^{n}(a_{i}-b_{i})^{2}.$

The squared form is a smooth, convex function of both points, and is widely used in optimization theory and statistics, forming the basis of least squares.

Euclidean distance in other coordinate systems

If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras' theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:

$x=r\cos \theta ,\ y=r\sin \theta .$

Then two points with locations (r₁, θ₁) and (r₂, θ₂) are separated by a distance s:

$s^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}=(r_{1}\cos \theta _{1}-r_{2}\cos \theta _{2})^{2}+(r_{1}\sin \theta _{1}-r_{2}\sin \theta _{2})^{2}.$

Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:

${\begin{aligned}s^{2}&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\left(\cos \theta _{1}\cos \theta _{2}+\sin \theta _{1}\sin \theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left(\theta _{1}-\theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \Delta \theta ,\end{aligned}}$

using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem. From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras' theorem is regained: $s^{2}=r_{1}^{2}+r_{2}^{2}.$ The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.

Pythagorean trigonometric identity

Artikel utama: Pythagorean trigonometric identity

Similar right triangles showing sine and cosine of angle θ

In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:

$\sin \theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.$

From that it follows:

${\cos }^{2}\theta +{\sin }^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}=1,$

where the last step applies Pythagoras' theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity. In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.

Relation to the cross product

The area of a parallelogram as a cross product; vectors a and b identify a plane and a × b is normal to this plane.

The Pythagorean theorem relates the cross product and dot product in a similar way:

$\|\mathbf {a} \times \mathbf {b} \|^{2}+(\mathbf {a} \cdot \mathbf {b} )^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}.$

This can be seen from the definitions of the cross product and dot product, as

${\begin{aligned}\mathbf {a} \times \mathbf {b} &=ab\mathbf {n} \sin {\theta }\\\mathbf {a} \cdot \mathbf {b} &=ab\cos {\theta },\end{aligned}}$

with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.

This can also be used to define the cross product. By rearranging the following equation is obtained

$\|\mathbf {a} \times \mathbf {b} \|^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.$

This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.

Generalizations

Similar figures on the three sides

A generalization of the Pythagorean theorem extending beyond the areas of squares on the three sides to similar figures was known by Hippocrates of Chios in the 5th century BC, and was included by Euclid in his Elements:

If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.

This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a:b:c). While Euclid's proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure's boundary being the side of the original triangle).

The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:

${\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,$

$\Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,.$

But, by the Pythagorean theorem, a² + b² = c², so A + B = C.

Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a² + b² = c². (See also Einstein's proof by dissection without rearrangement)

Generalization for similar triangles,green area A + B = blue area C

Pythagoras' theorem using similar right triangles

Generalization for regular pentagons

Law of cosines

The separation s of two points (r₁, θ₁) and (r₂, θ₂) in polar coordinates is given by the law of cosines. Interior angle Δθ = θ₁−θ₂.

Artikel utama: Law of cosines

The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:

$a^{2}+b^{2}-2ab\cos {\theta }=c^{2},$

where $\theta$ is the angle between sides $a$ and $b$.

When $\theta$ is ${\frac {\pi }{2}}$ radians or 90°, then $\cos {\theta }=0$, and the formula reduces to the usual Pythagorean theorem.

Arbitrary triangle

Generalization of Pythagoras' theorem by Tâbit ibn Qorra. Lower panel: reflection of triangle CAD (top) to form triangle DAC, similar to triangle ABC (top).

At any selected angle of a general triangle of sides a, b, c, inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled c. Inscribing the isosceles triangle forms triangle CAD with angle θ opposite side b and with side r along c. A second triangle is formed with angle θ opposite side a and a side with length s along c, as shown in the figure. Thābit ibn Qurra stated that the sides of the three triangles were related as:

$a^{2}+b^{2}=c(r+s)\ .$

As the angle θ approaches π/2, the base of the isosceles triangle narrows, and lengths r and s overlap less and less. When θ = π/2, ADB becomes a right triangle, r + s = c, and the original Pythagorean theorem is regained.

One proof observes that triangle ABC has the same angles as triangle CAD, but in opposite order. (The two triangles share the angle at vertex A, both contain the angle θ, and so also have the same third angle by the triangle postulate.) Consequently, ABC is similar to the reflection of CAD, the triangle DAC in the lower panel. Taking the ratio of sides opposite and adjacent to θ,

${\frac {c}{b}}={\frac {b}{r}}\ .$

Likewise, for the reflection of the other triangle,

${\frac {c}{a}}={\frac {a}{s}}\ .$

Clearing fractions and adding these two relations:

$cs+cr=a^{2}+b^{2}\ ,$

the required result.

The theorem remains valid if the angle $\theta$ is obtuse so the lengths r and s are non-overlapping.

General triangles using parallelograms

Generalization for arbitrary triangles,green area = blue area

Construction for proof of parallelogram generalization

Pappus's area theorem is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares (squares are a special case, of course). The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras' theorem, and was considered a generalization by Pappus of Alexandria in 4 AD

The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base b and height h. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms.

Solid geometry

Artikel utama: Solid geometry

Pythagoras' theorem in three dimensions relates the diagonal AD to the three sides.

A tetrahedron with outward facing right-angle corner

In terms of solid geometry, Pythagoras' theorem can be applied to three dimensions as follows. Consider a rectangular solid as shown in the figure. The length of diagonal BD is found from Pythagoras' theorem as:

${\overline {BD}}^{\,2}={\overline {BC}}^{\,2}+{\overline {CD}}^{\,2}\ ,$

where these three sides form a right triangle. Using horizontal diagonal BD and the vertical edge AB, the length of diagonal AD then is found by a second application of Pythagoras' theorem as:

${\overline {AD}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BD}}^{\,2}\ ,$

or, doing it all in one step:

${\overline {AD}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BC}}^{\,2}+{\overline {CD}}^{\,2}\ .$

This result is the three-dimensional expression for the magnitude of a vector v (the diagonal AD) in terms of its orthogonal components {v_k} (the three mutually perpendicular sides):

$\|\mathbf {v} \|^{2}=\sum _{k=1}^{3}\|\mathbf {v} _{k}\|^{2}.$

This one-step formulation may be viewed as a generalization of Pythagoras' theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras' theorem to a succession of right triangles in a sequence of orthogonal planes.

A substantial generalization of the Pythagorean theorem to three dimensions is de Gua's theorem, named for Jean Paul de Gua de Malves: If a tetrahedron has a right angle corner (like a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the "n-dimensional Pythagorean theorem":

Let $x_{1},x_{2},\ldots ,x_{n}$ be orthogonal vectors in ℝⁿ. Consider the n-dimensional simplex S with vertices $0,x_{1},\ldots ,x_{n}$. (Think of the (n − 1)-dimensional simplex with vertices $x_{1},\ldots ,x_{n}$ not including the origin as the "hypotenuse" of S and the remaining (n − 1)-dimensional faces of S as its "legs".) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.

This statement is illustrated in three dimensions by the tetrahedron in the figure. The "hypotenuse" is the base of the tetrahedron at the back of the figure, and the "legs" are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the "legs" increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras' theorem applies. In a different wording:

Given an n-rectangular n-dimensional simplex, the square of the (n − 1)-content of the facet opposing the right vertex will equal the sum of the squares of the (n − 1)-contents of the remaining facets.

Inner product spaces

Lihat pula: Hilbert space

Vectors involved in the parallelogram law

The Pythagorean theorem can be generalized to inner product spaces, which are generalizations of the familiar 2-dimensional and 3-dimensional Euclidean spaces. For example, a function may be considered as a vector with infinitely many components in an inner product space, as in functional analysis.

In an inner product space, the concept of perpendicularity is replaced by the concept of orthogonality: two vectors v and w are orthogonal if their inner product $\langle \mathbf {v} ,\mathbf {w} \rangle$ is zero. The inner product is a generalization of the dot product of vectors. The dot product is called the standard inner product or the Euclidean inner product. However, other inner products are possible.

The concept of length is replaced by the concept of the norm ||v|| of a vector v, defined as:

$\lVert \mathbf {v} \rVert \equiv {\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}\,.$

In an inner-product space, the Pythagorean theorem states that for any two orthogonal vectors v and w we have

$\left\|\mathbf {v} +\mathbf {w} \right\|^{2}=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2}.$

Here the vectors v and w are akin to the sides of a right triangle with hypotenuse given by the vector sum v + w. This form of the Pythagorean theorem is a consequence of the properties of the inner product:

$\left\|\mathbf {v} +\mathbf {w} \right\|^{2}=\langle \mathbf {v+w} ,\ \mathbf {v+w} \rangle =\langle \mathbf {v} ,\ \mathbf {v} \rangle +\langle \mathbf {w} ,\ \mathbf {w} \rangle +\langle \mathbf {v,\ w} \rangle +\langle \mathbf {w,\ v} \rangle \ =\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2},$

where the inner products of the cross terms are zero, because of orthogonality.

A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the parallelogram law :

$2\|\mathbf {v} \|^{2}+2\|\mathbf {w} \|^{2}=\|\mathbf {v+w} \|^{2}+\|\mathbf {v-w} \|^{2}\ ,$

which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is ipso facto a norm corresponding to an inner product.

The Pythagorean identity can be extended to sums of more than two orthogonal vectors. If v₁, v₂, ..., v_n are pairwise-orthogonal vectors in an inner-product space, then application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on solid geometry) results in the equation

$\left\|\sum _{k=1}^{n}\mathbf {v} _{k}\right\|^{2}=\sum _{k=1}^{n}\|\mathbf {v} _{k}\|^{2}$

Sets of m-dimensional objects in n-dimensional space

Another generalization of the Pythagorean theorem applies to Lebesgue-measurable sets of objects in any number of dimensions. Specifically, the square of the measure of an m-dimensional set of objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space is equal to the sum of the squares of the measures of the orthogonal projections of the object(s) onto all m-dimensional coordinate subspaces.

In mathematical terms:

$\mu _{ms}^{2}=\sum _{i=1}^{x}\mathbf {\mu ^{2}} _{mp_{i}}$

where:

• $\mu _{m}$ is a measure in m-dimensions (a length in one dimension, an area in two dimensions, a volume in three dimensions, etc.).
• $s$ is a set of one or more non-overlapping m-dimensional objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space.
• $\mu _{ms}$ is the total measure (sum) of the set of m-dimensional objects.
• $p$ represents an m-dimensional projection of the original set onto an orthogonal coordinate subspace.
• $\mu _{mp_{i}}$ is the measure of the m-dimensional set projection onto m-dimensional coordinate subspace $i$. Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace.
• $x$ is the number of orthogonal, m-dimensional coordinate subspaces in n-dimensional space (Rⁿ) onto which the m-dimensional objects are projected (m ≤ n):

$x={\binom {n}{m}}={\frac {n!}{m!(n-m)!}}$

Non-Euclidean geometry

Artikel utama: Non-Euclidean geometry

Lihat pula: Hilbert's axioms

The Pythagorean theorem is derived from the axioms of Euclidean geometry, and in fact, were the Pythagorean theorem to fail for some right triangle, then the plane in which this triangle is contained cannot be Euclidean. More precisely, the Pythagorean theorem implies, and is implied by, Euclid's Parallel (Fifth) Postulate. Thus, right triangles in a non-Euclidean geometry do not satisfy the Pythagorean theorem. For example, in spherical geometry, all three sides of the right triangle (say a, b, and c) bounding an octant of the unit sphere have length equal to π/2, and all its angles are right angles, which violates the Pythagorean theorem because $a^{2}+b^{2}=2c^{2}>c^{2}$.

Here two cases of non-Euclidean geometry are considered—spherical geometry and hyperbolic plane geometry; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines.

However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say A+B = C. The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c.

Spherical geometry

Artikel utama: Spherical geometry

Spherical triangle

For any right triangle on a sphere of radius R (for example, if γ in the figure is a right angle), with sides a, b, c, the relation between the sides takes the form:

$\cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cos \left({\frac {b}{R}}\right).$

This equation can be derived as a special case of the spherical law of cosines that applies to all spherical triangles:

$\cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cos \left({\frac {b}{R}}\right)+\sin \left({\frac {a}{R}}\right)\sin \left({\frac {b}{R}}\right)\cos \gamma \ .$

By expressing the Maclaurin series for the cosine function as an asymptotic expansion with the remainder term in big O notation,

$\cos x=1-{\frac {x^{2}}{2}}+O(x^{4}){\text{ as }}x\to 0\ ,$

it can be shown that as the radius R approaches infinity and the arguments a/R, b/R, and c/R tend to zero, the spherical relation between the sides of a right triangle approaches the Euclidean form of the Pythagorean theorem. Substituting the asymptotic expansion for each of the cosines into the spherical relation for a right triangle yields

$1-{\frac {1}{2}}\left({\frac {c}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)=\left[1-{\frac {1}{2}}\left({\frac {a}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)\right]\left[1-{\frac {1}{2}}\left({\frac {b}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)\right]{\text{ as }}R\to \infty \ .$

The constants a⁴, b⁴, and c⁴ have been absorbed into the big O remainder terms since they are independent of the radius R. This asymptotic relationship can be further simplified by multiplying out the bracketed quantities, cancelling the ones, multiplying through by −2, and collecting all the error terms together:

$\left({\frac {c}{R}}\right)^{2}=\left({\frac {a}{R}}\right)^{2}+\left({\frac {b}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right){\text{ as }}R\to \infty \ .$

After multiplying through by R², the Euclidean Pythagorean relationship c² = a² + b² is recovered in the limit as the radius R approaches infinity (since the remainder term tends to zero):

$c^{2}=a^{2}+b^{2}+O\left({\frac {1}{R^{2}}}\right){\text{ as }}R\to \infty \ .$

For small right triangles (a, b << R), the cosines can be eliminated to avoid loss of significance, giving

$\sin ^{2}{\frac {c}{2R}}=\sin ^{2}{\frac {a}{2R}}+\sin ^{2}{\frac {b}{2R}}-2\sin ^{2}{\frac {a}{2R}}\sin ^{2}{\frac {b}{2R}}\,.$

Hyperbolic geometry

Artikel utama: Hyperbolic geometry

Lihat pula: Hyperbolic triangle dan Gaussian curvature

Hyperbolic triangle

In a hyperbolic space with uniform curvature −1/R², for a right triangle with legs a, b, and hypotenuse c, the relation between the sides takes the form:

$\cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\,\cosh {\frac {b}{R}}$

where cosh is the hyperbolic cosine. This formula is a special form of the hyperbolic law of cosines that applies to all hyperbolic triangles:

$\cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\ \cosh {\frac {b}{R}}-\sinh {\frac {a}{R}}\ \sinh {\frac {b}{R}}\ \cos \gamma \ ,$

with γ the angle at the vertex opposite the side c.

By using the Maclaurin series for the hyperbolic cosine, cosh x ≈ 1 + x²/2, it can be shown that as a hyperbolic triangle becomes very small (that is, as a, b, and c all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras' theorem.

For small right triangles (a, b << R), the hyperbolic cosines can be eliminated to avoid loss of significance, giving

$\sinh ^{2}{\frac {c}{2R}}=\sinh ^{2}{\frac {a}{2R}}+\sinh ^{2}{\frac {b}{2R}}+2\sinh ^{2}{\frac {a}{2R}}\sinh ^{2}{\frac {b}{2R}}\,.$

Very small triangles

For any uniform curvature K (positive, zero, or negative), in very small right triangles (|K|a², |K|b² << 1) with hypotenuse c, it can be shown that

$c^{2}=a^{2}+b^{2}-{\frac {K}{3}}a^{2}b^{2}-{\frac {K^{2}}{45}}a^{2}b^{2}(a^{2}+b^{2})-{\frac {2K^{3}}{945}}a^{2}b^{2}(a^{2}-b^{2})^{2}+O(K^{4}c^{10})\,.$

Differential geometry

Artikel utama: Differential geometry

Distance between infinitesimally separated points in Cartesian coordinates (top) and polar coordinates (bottom), as given by Pythagoras' theorem

On an infinitesimal level, in three dimensional space, Pythagoras' theorem describes the distance between two infinitesimally separated points as:

$ds^{2}=dx^{2}+dy^{2}+dz^{2},$

with ds the element of distance and (dx, dy, dz) the components of the vector separating the two points. Such a space is called a Euclidean space. However, in Riemannian geometry, a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:

$ds^{2}=\sum _{i,j}^{n}g_{ij}\,dx_{i}\,dx_{j}$

which is called the metric tensor. (Sometimes, by abuse of language, the same term is applied to the set of coefficients g_ij.) It may be a function of position, and often describes curved space. A simple example is Euclidean (flat) space expressed in curvilinear coordinates. For example, in polar coordinates:

$ds^{2}=dr^{2}+r^{2}d\theta ^{2}\ .$

History

The Plimpton 322 tablet records Pythagorean triples from Babylonian times.

There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BC), over a thousand years before Pythagoras was born. The history of the theorem can be divided into four parts: knowledge of Pythagorean triples, knowledge of the relationship among the sides of a right triangle, knowledge of the relationships among adjacent angles, and proofs of the theorem within some deductive system.

Written between 2000 and 1786 BC, the Egyptian Middle Kingdom Berlin Papyrus 6619 includes a problem whose solution is the Pythagorean triple 6:8:10, but the problem does not mention a triangle. The Mesopotamian tablet Plimpton 322, written between 1790 and 1750 BC during the reign of King Hammurabi the Great, contains many entries closely related to Pythagorean triples.

In India, the Baudhayana Shulba Sutra, the dates of which are given variously as between the 8th and 5th century BC, contains a list of Pythagorean triples and a statement of the Pythagorean theorem, both in the special case of the isosceles right triangle and in the general case, as does the Apastamba Shulba Sutra (c. 600 BC).

Byzantine Neoplatonic philosopher and mathematician Proclus, writing in the fifth century AD, states two arithmetic rules, "one of them attributed to Plato, the other to Pythagoras", for generating special Pythagorean triples. The rule attributed to Pythagoras (ca 570–ca 495 BC) starts from an odd number and produces a triple with leg and hypotenuse differing by one unit; the rule attributed to Plato (428/427 or 424/423 – 348/347 BC) starts from an even number and produces a triple with leg and hypotenuse differing by two units. According to Thomas L. Heath (1861–1940), no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived. However, when authors such as Plutarch and Cicero attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted. Classicist Kurt von Fritz wrote, "Whether this formula is rightly attributed to Pythagoras personally, but one can safely assume that it belongs to the very oldest period of Pythagorean mathematics." Around 300 BC, in Euclid's Elements, the oldest extant axiomatic proof of the theorem is presented.

Geometric proof of the Pythagorean theorem from the Zhoubi Suanjing.

With contents known much earlier, but in surviving texts dating from roughly the 1st century BC, the Chinese text Zhoubi Suanjing (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives a reasoning for the Pythagorean theorem for the (3, 4, 5) triangle — in China it is called the "Gougu theorem" (勾股定理). During the Han Dynasty (202 BC to 220 AD), Pythagorean triples appear in The Nine Chapters on the Mathematical Art, together with a mention of right triangles. Some believe the theorem arose first in China, where it is alternatively known as the "Shang Gao theorem" (商高定理), named after the Duke of Zhou's astronomer and mathematician, whose reasoning composed most of what was in the Zhoubi Suanjing.

See also

• Addition in quadrature
• At Dulcarnon
• British flag theorem
• Fermat's Last Theorem
• Inverse Pythagorean theorem
• Kepler triangle
• Linear algebra
• List of triangle topics
• L^p space
• Nonhypotenuse number
• Parallelogram law
• Parseval's identity
• Ptolemy's theorem
• Pythagorean expectation
• Pythagorean tiling
• Rational trigonometry in Pythagoras' theorem
• Thales theorem

Catatan kaki dan rujukan

Kutipan

• Loomis, Elisha Scott (1968). The Pythagorean proposition (edisi ke-2nd). The National Council of Teachers of Mathematics. ISBN 978-0-87353-036-1.  For full text of 2nd edition of 1940, see Elisha Scott Loomis. "The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs" (PDF). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Diakses tanggal 2010-05-04.  Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, ISBN 0-87353-036-5.