Kubus

Halaman ini berisi artikel tentang bentuk 3 dimensi. Untuk kubus dalam dimensi apapun, lihat Hiperkubus. Untuk penggunaan lainnya, lihat Kubus (disambiguasi).

Dalam geometri, kubusec adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk, dan 8 titik sudut. Kubus juga disebut dengan bidang enam beraturan, selain itu kubus juga merupakan bentuk khusus dalam prisma segi empat, [1].

Kubus
Kubus berbentuk Hexahedron
Jenis	Padat platonis
Muka	6
Rusuk	12
titik sudut	8
Konfigurasi titik sudut	V 3.3.3.3
Simbol Wythoff	3
Simbol Schläfli	{4,3}
Diagram Coxeter
Grup simetri	Oh, B3, [4,3], (* 432)
Sudut dihedral (derajat)	90°
Sifat-sifat	reguler, cembung zonohedron
Jaring

Net of a cube

Kubus dalam 3D

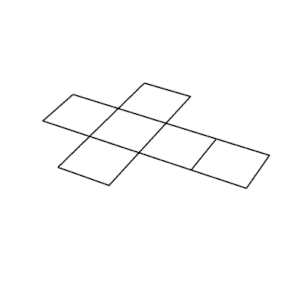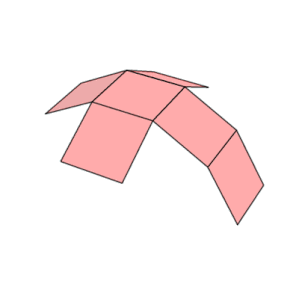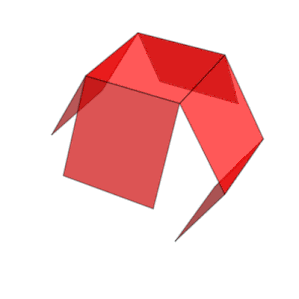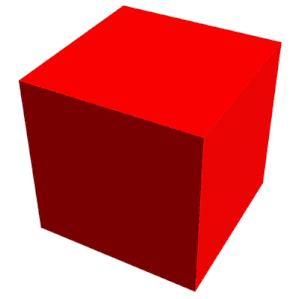
Proyeksi ortogonal

Kubus memiliki empat khusus proyeksi orthogonal , berpusat, pada titik, tepi, wajah dan normal nya angka vertex . Yang pertama dan ketiga sesuai dengan Diagram Coxeter A₂ dan B₂

Proyeksi ortogonal

Dipusatkan oleh	Wajah	Vertex
Diagram Coxeter	B2	A2
Projective symmetry	[4]	[6]
Tilted views

Ubin bulat

Kubus juga dapat direpresentasikan sebagai ubin bola, dan diproyeksikan ke pesawat melalui proyeksi stereografi. Proyeksi ini konformal, menjaga sudut tetapi bukan area atau panjang. Garis lurus pada bola diproyeksikan sebagai busur melingkar di pesawat.

Proyeksi ortografis	Proyeksi stereografi

Kordinat kartesius

Untuk sebuah kubus yang berpusat di titik asal, dengan tepi sejajar dengan sumbu dan dengan panjang tepi 2, koordinat kartesius dari simpul adalah

(±1, ±1, ±1)

sedangkan interior terdiri dari semua titik (x₀, x₁, x₂) with −1 < x_i < 1 for all i.

Persamaan dalam $\mathbb {R} ^{3}$

Dalam geometri analitik , permukaan kubus dengan pusat (x₀, y₀, z₀) dan panjang tepi 2a adalah lokus semua titik (x, y, z) sedemikian rupa sehingga

$\max\{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|\}=a.$

Sebuah kubus juga dapat dianggap sebagai kasus pembatas superellipsoid 3D karena ketiga eksponen mendekati tak terhingga.

Rumus

Bila variabel S adalah panjang rusuk kubus, maka:

Luas permukaan

$L=6\cdot S^{2}$

Volume

$V=\ S^{3}=Sisi^{3}$

Diagonal sisi

$d_{S}=S{\sqrt {2}}$

Diagonal sisi seluruhnya

$d_{Ss}=12\cdot S{\sqrt {2}}$

Diagonal ruang

$d_{R}=S{\sqrt {3}}$

Diagonal ruang seluruhnya

$d_{Rs}=4\cdot S{\sqrt {3}}$

Luas bidang diagonal

$L_{B}=S^{2}{\sqrt {2}}$

Luas bidang diagonal seluruhnya

$L_{Bs}=6\cdot S^{2}{\sqrt {2}}$

Tunjuk ruang

Untuk kubus yang bulatan pembatasnya memiliki jari-jari R, dan untuk titik tertentu dalam ruang 3-dimensi dengan jarak d_i dari delapan simpul kubus, kita memiliki:

${\frac {\sum _{i=1}^{8}d_{i}^{4}}{8}}+{\frac {16R^{4}}{9}}=\left({\frac {\sum _{i=1}^{8}d_{i}^{2}}{8}}+{\frac {2R^{2}}{3}}\right)^{2}.$

Menggandakan kubus

Menggandakan kubus, atau masalah Delian, adalah masalah yang ditimbulkan oleh ahli matematika Yunani kuno hanya menggunakan kompas dan penggaris-sejajar untuk memulai dengan panjang tepi kubus yang diberikan dan untuk membangun panjang tepi kubus dengan dua kali lipat volume kubus asli. Mereka tidak dapat menyelesaikan masalah ini, dan pada tahun 1837 Pierre Wantzel membuktikannya tidak mungkin karena akar pangkat dua bukanlah angka yang dapat dibangun.

Pewarnaan dan simetri yang seragam

Pohon simetri oktahedral

Kubus memiliki tiga warna yang seragam, dinamai dengan warna wajah persegi di sekitar setiap titik: 111, 112, 123.

Kubus memiliki empat kelas simetri, yang dapat diwakili oleh pewarnaan verteks-transitif wajah. Simetri oktahedral tertinggi O_h memiliki semua wajah dengan warna yang sama. Dihedral simetri D_4h berasal dari kubus menjadi prisma, dengan keempat sisinya menjadi warna yang sama. Himpunan bagian prismatik D_2d memiliki warna yang sama dengan yang sebelumnya dan D_2h memiliki warna bergantian untuk sisinya dengan total tiga warna, dipasangkan oleh sisi yang berlawanan. Setiap bentuk simetri memiliki Simbol Wythoff yang berbeda.

Nama	Heksahedron biasa	Prisma persegi	Trapesium persegi panjang	Balok	Rhombic prisma	Trigonal trapezohedron
Coxeter diagram
Schläfli symbol	{4,3}	{4}×{ } rr{4,2}	s2{2,4}	{ }3 tr{2,2}	{ }×2{ }
Wythoff symbol	3 | 4 2	4 2 | 2		2 2 2 |
Symmetry	Oh [4,3] (*432)	D4h [4,2] (*422)	D2d [4,2+] (2*2)	D2h [2,2] (*222)		D3d [6,2+] (2*3)
Symmetry order	24	16	8	8		12
Image (uniform coloring)	(111)	(112)	(112)	(123)	(112)	(111), (112)

Grafik

–⟩ Lihat pula:Paralelipiped

Kerangka kubus (simpul dan tepi) membentuk grafik , dengan 8 simpul, dan 12 tepi. Ini adalah kasus khusus dari grafik Kubushiper. Ini adalah salah satu dari 5 grafik Platonis , masing-masing merupakan kerangka dari padatan Platoniknya.

Perpanjangan adalah grafik tiga dimensi k -ary Hamming , yang untuk k = 2 adalah grafik kubus. Grafik semacam ini muncul dalam teori pemrosesan paralel di komputer.

Pranala luar

• Weisstein, Eric W. "Cube". MathWorld. 
• Cube: Interactive Polyhedron Model
• Volume kubus, dengan animasi interaktif
• Cube (Situs Robert Webb)