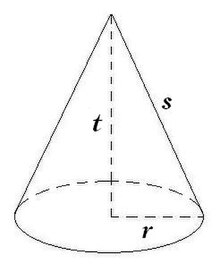
Dalam geometri , kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut mempunyai 2 sisi, 1 rusuk, dan 1 titik sudut.
Sebuah kerucut dengan tinggi (t s Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang miring yang disebut selimut kerucut.
Keliling dasar kerucut disebut "directrix", dan masing-masing segmen garis antara directrix dan apex adalah "generatrix" atau "garis pembangkit" dari permukaan lateral. (Untuk hubungan antara pengertian istilah "directrix" dan directrix dari bagian kerucut, lihat Dandelin spheres .)
"Jari-jari dasar" dari kerucut lingkaran adalah jari - jari alasnya; sering kali ini hanya disebut jari-jari kerucut. The aperture kerucut melingkar tepat adalah sudut maksimum antara dua garis generatrix; jika generatrix membuat sudut θ ke sumbu, aperture adalah 2 θ .
Ilustrasi dari Problemata Mathematica ... diterbitkan dalam Acta Eruditorum , 1734 Sebuah kerucut dengan daerah termasuk puncaknya dipotong oleh pesawat disebut " kerucut terpotong "; jika bidang pemotongan sejajar dengan basis kerucut, itu disebut frustum .[ 1] [ 1]
s
=
r
2
+
t
2
{\displaystyle s={\sqrt {r^{2}+t^{2}}}}
L
=
π
r
2
{\displaystyle L=\pi r^{2}}
L
=
π
r
s
{\displaystyle L=\pi rs}
=
π
r
r
2
+
t
2
{\displaystyle =\pi r{\sqrt {r^{2}+t^{2}}}}
L
=
L
a
+
L
s
{\displaystyle L=L_{a}+L_{s}}
=
π
r
2
+
π
r
s
{\displaystyle =\pi r^{2}+\pi rs}
=
π
r
⋅
(
r
+
s
)
{\displaystyle =\pi r\cdot (r+s)}
=
π
r
⋅
(
r
+
r
2
+
t
2
)
{\displaystyle =\pi r\cdot (r+{\sqrt {r^{2}+t^{2}}})}
Volume kerucut dapat dirumuskan sebagai berikut
V
=
1
3
⋅
π
r
2
⋅
t
{\displaystyle V={\frac {1}{3}}\cdot \pi r^{2}\cdot t}
dimana
r
{\displaystyle r}
h
{\displaystyle h}
jari-jari dan tinggi kerucut.
Untuk membuktikan rumus volume kerucut di atas, berikut ini merupakan pembuktian di antaranya:
Kerucut yang di dalamnya adalah segitiga (Merah), sebagai bentuk revolusi Bukti volume kerucut melalui kalkulus
sunting
Misal
y
=
r
x
h
{\displaystyle y={\frac {rx}{h}}}
r
>
0
{\displaystyle r>0}
h
>
0
{\displaystyle h>0}
x
{\displaystyle x}
x
=
h
{\displaystyle x=h}
x
{\displaystyle x}
Δ
V
=
π
(
r
h
x
)
2
Δ
x
{\displaystyle \Delta V=\pi \left({\frac {r}{h}}x\right)^{2}\,\Delta x}
lalu, mengintegrasikannya
V
=
π
r
2
h
2
∫
0
h
x
2
d
x
=
π
r
2
h
2
[
x
3
3
]
0
h
=
1
3
π
r
2
h
{\displaystyle V={\frac {\pi r^{2}}{h^{2}}}\int _{0}^{h}x^{2}\,\mathrm {d} x={\frac {\pi r^{2}}{h^{2}}}\left[{\frac {x^{3}}{3}}\right]_{0}^{h}={\frac {1}{3}}\pi r^{2}h}
[ 2]
Kerucut bundar padat yang tepat dengan tinggi
h
{\displaystyle h}
2
θ
{\displaystyle 2\theta }
z
{\displaystyle z}
F
(
s
,
t
,
u
)
=
(
u
tan
s
cos
t
,
u
tan
s
sin
t
,
u
)
{\displaystyle F(s,t,u)=\left(u\tan s\cos t,u\tan s\sin t,u\right)}
dimana
s
,
t
,
u
{\displaystyle s,t,u}
[
0
,
θ
)
{\displaystyle [0,\theta )}
[
0
,
2
π
)
{\displaystyle [0,2\pi )}
[
0
,
h
]
{\displaystyle [0,h]}
Dalam bentuk tersirat , padatan yang sama didefinisikan oleh ketidaksetaraan
{
F
(
x
,
y
,
z
)
≤
0
,
z
≥
0
,
z
≤
h
}
,
{\displaystyle \{F(x,y,z)\leq 0,z\geq 0,z\leq h\},}
dimana
F
(
x
,
y
,
z
)
=
(
x
2
+
y
2
)
(
cos
θ
)
2
−
z
2
(
sin
θ
)
2
.
{\displaystyle F(x,y,z)=(x^{2}+y^{2})(\cos \theta )^{2}-z^{2}(\sin \theta )^{2}.\,}
Lebih umum, kerucut melingkar kanan dengan titik pada asal, sumbu sejajar dengan vektor
2
θ
{\displaystyle 2\theta }
vektor implisit
F
(
u
)
=
0
{\displaystyle F(u)=0}
F
(
u
)
=
(
u
⋅
d
)
2
−
(
d
⋅
d
)
(
u
⋅
u
)
(
cos
θ
)
2
{\displaystyle F(u)=(u\cdot d)^{2}-(d\cdot d)(u\cdot u)(\cos \theta )^{2}}
F
(
u
)
=
u
⋅
d
−
|
d
|
|
u
|
cos
θ
{\displaystyle F(u)=u\cdot d-|d||u|\cos \theta }
dimana
u
=
(
x
,
y
,
z
)
{\displaystyle u=(x,y,z)}
u
⋅
d
{\displaystyle u\cdot d}
Permukaan quartic dan elips Dalam sistem koordinat Kartesius ,sebuah kerucut elips adalah lokus dari persamaan bentuk [ 3]
x
2
a
2
+
y
2
b
2
=
z
2
.
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=z^{2}.}
Ini adalah sebuah gambar affine dari unit lingkaran kanan dengan persamaan
x
2
+
y
2
=
z
2
.
{\displaystyle x^{2}+y^{2}=z^{2}\ .}
elips , parabola , ...) orang mendapat:
Setiap bagian pesawat kerucut elips adalah bagian kerucut. Jelas, setiap kerucut melingkar kanan berisi lingkaran. Ini juga benar, tetapi kurang jelas, dalam kasus umum
Representasi parameter kerucut dapat dijelaskan sebagai berikut. Dengan gambar
P
→
{\displaystyle {\overrightarrow {P}}}
Q
→
{\displaystyle {\overrightarrow {Q}}}
P
→
(
γ
,
φ
,
χ
)
=
(
x
y
z
)
=
χ
⋅
(
γ
cos
(
φ
)
γ
sin
(
φ
)
1
)
Q
→
(
x
,
y
,
z
)
=
(
γ
φ
χ
)
=
(
1
z
x
2
+
y
2
arctan
2
(
y
,
x
)
z
)
{\displaystyle {\overrightarrow {P}}(\gamma ,\varphi ,\chi )={\begin{pmatrix}x\\y\\z\end{pmatrix}}=\chi \cdot {\begin{pmatrix}\gamma \cos(\varphi )\\\gamma \sin(\varphi )\\1\end{pmatrix}}\quad \quad \quad {\overrightarrow {Q}}(x,y,z)={\begin{pmatrix}\gamma \\\varphi \\\chi \end{pmatrix}}={\begin{pmatrix}{\frac {1}{z}}{\sqrt {x^{2}+y^{2}}}\\\arctan 2(y,x)\\z\end{pmatrix}}}
Konversi segmen kerucut yang diberikan ke koordinat kerucut
sunting
Segmen kerucut dengan tinggi h dan jari-jari r1 dan r2 Keliling segmen kerucut diberikan oleh (lihat ilustrasi di bawah):
r
1
≤
r
≤
r
2
0
≤
φ
≤
2
π
h
=
z
2
−
z
1
{\displaystyle r_{1}\leq r\leq r_{2}\quad \quad \quad 0\leq \varphi \leq 2\pi \quad \quad \quad h=z_{2}-z_{1}}
Maka batasnya dapat dinyatakan dalam keliling kerucut sebagai berikut:
γ
1
=
r
2
−
r
1
h
χ
1
=
r
1
γ
1
=
h
⋅
r
1
r
2
−
r
1
χ
2
=
r
2
γ
1
=
h
⋅
r
2
r
2
−
r
1
{\displaystyle \gamma _{1}={\frac {r_{2}-r_{1}}{h}}\quad \quad \chi _{1}={\frac {r_{1}}{\gamma _{1}}}=h\cdot {\frac {r_{1}}{r_{2}-r_{1}}}\quad \quad \chi _{2}={\frac {r_{2}}{\gamma _{1}}}=h\cdot {\frac {r_{2}}{r_{2}-r_{1}}}}
Keliling segmen kerucut padat karenanya berkisar:
0
≤
γ
≤
γ
1
0
≤
φ
≤
2
π
χ
1
≤
χ
≤
χ
2
{\displaystyle 0\leq \gamma \leq \gamma _{1}\quad \quad \quad 0\leq \varphi \leq 2\pi \quad \quad \quad \chi _{1}\leq \chi \leq \chi _{2}}
Representasi keliling berikut ini berlaku untuk permukaan lateral yang sesuai dari segmen kerucut ini:
γ
=
γ
1
0
≤
φ
≤
2
π
χ
1
≤
χ
≤
χ
2
{\displaystyle \gamma =\gamma _{1}\quad \quad \quad 0\leq \varphi \leq 2\pi \quad \quad \quad \chi _{1}\leq \chi \leq \chi _{2}}
Vektor normal permukaan adalah ortogonal ke permukaan kerucut. Diperlukan untuk B . melakukan perhitungan aliran melalui permukaan lateral. Luas permukaan lateral dapat dihitung sebagai integral ganda menggunakan norma vektor normal permukaan.
n
→
=
∂
P
→
∂
φ
×
∂
P
→
∂
χ
=
χ
γ
⋅
(
cos
(
φ
)
sin
(
φ
)
−
γ
)
{\displaystyle {\overrightarrow {n}}={\frac {\partial {\overrightarrow {P}}}{\partial \varphi }}\times {\frac {\partial {\overrightarrow {P}}}{\partial \chi }}=\chi \gamma \cdot {\begin{pmatrix}\cos(\varphi )\\\sin(\varphi )\\-\gamma \end{pmatrix}}}
Vektor satuan koordinat kerucut dalam komponen kartesius
sunting
Vektor satuan dalam komponen kartesius diperoleh dengan normalisasi pada vektor tangen dari parameterisasi tersebut. Vektor tangen dihasilkan dari turunan parsial pertama menurut masing-masing variabel. Ketiga vektor satuan ini membentuk basis normal. Ini bukan basis ortonormal karena tidak semua vektor satuan ortogonal satu sama lain.
e
γ
→
=
∂
γ
P
→
‖
∂
γ
P
→
‖
=
(
cos
(
φ
)
sin
(
φ
)
0
)
e
φ
→
=
∂
φ
P
→
‖
∂
φ
P
→
‖
=
(
−
sin
(
φ
)
cos
(
φ
)
0
)
e
χ
→
=
∂
χ
P
→
‖
∂
χ
P
→
‖
=
1
1
+
γ
2
(
γ
cos
(
φ
)
γ
sin
(
φ
)
1
)
{\displaystyle {\overrightarrow {e_{\gamma }}}={\frac {\partial _{\gamma }{\overrightarrow {P}}}{\left\|\partial _{\gamma }{\overrightarrow {P}}\right\|}}={\begin{pmatrix}\cos(\varphi )\\\sin(\varphi )\\0\end{pmatrix}}\quad \quad {\overrightarrow {e_{\varphi }}}={\frac {\partial _{\varphi }{\overrightarrow {P}}}{\left\|\partial _{\varphi }{\overrightarrow {P}}\right\|}}={\begin{pmatrix}-\sin(\varphi )\\\cos(\varphi )\\0\end{pmatrix}}\quad \quad {\overrightarrow {e_{\chi }}}={\frac {\partial _{\chi }{\overrightarrow {P}}}{\left\|\partial _{\chi }{\overrightarrow {P}}\right\|}}={\frac {1}{\sqrt {1+\gamma ^{2}}}}{\begin{pmatrix}\gamma \cos(\varphi )\\\gamma \sin(\varphi )\\1\end{pmatrix}}}
Matriks fungsional dan kebalikannya diperlukan untuk kemudian mengubah turunan parsial.
J
f
=
∂
(
x
,
y
,
z
)
∂
(
γ
,
φ
,
χ
)
=
(
∂
γ
x
∂
φ
x
∂
χ
x
∂
γ
y
∂
φ
y
∂
χ
y
∂
γ
z
∂
φ
z
∂
χ
z
)
=
(
χ
cos
(
φ
)
−
χ
γ
sin
(
φ
)
γ
cos
(
φ
)
χ
sin
(
φ
)
χ
γ
cos
(
φ
)
γ
sin
(
φ
)
0
0
1
)
{\displaystyle J_{f}={\frac {\partial \left(x,y,z\right)}{\partial \left(\gamma ,\varphi ,\chi \right)}}={\begin{pmatrix}\partial _{\gamma }x&\partial _{\varphi }x&\partial _{\chi }x\\\partial _{\gamma }y&\partial _{\varphi }y&\partial _{\chi }y\\\partial _{\gamma }z&\partial _{\varphi }z&\partial _{\chi }z\end{pmatrix}}={\begin{pmatrix}\chi \cos(\varphi )&-\chi \gamma \sin(\varphi )&\gamma \cos(\varphi )\\\chi \sin(\varphi )&\chi \gamma \cos(\varphi )&\gamma \sin(\varphi )\\0&0&1\end{pmatrix}}}
J
f
−
1
=
∂
(
γ
,
φ
,
χ
)
∂
(
x
,
y
,
z
)
=
(
∂
x
γ
∂
y
γ
∂
z
γ
∂
x
φ
∂
y
φ
∂
z
φ
∂
x
χ
∂
y
χ
∂
z
χ
)
=
(
cos
(
φ
)
χ
sin
(
φ
)
χ
−
γ
χ
−
sin
(
φ
)
χ
γ
cos
(
φ
)
χ
γ
0
0
0
1
)
{\displaystyle J_{f}^{-1}={\frac {\partial \left(\gamma ,\varphi ,\chi \right)}{\partial \left(x,y,z\right)}}={\begin{pmatrix}\partial _{x}\gamma &\partial _{y}\gamma &\partial _{z}\gamma \\\partial _{x}\varphi &\partial _{y}\varphi &\partial _{z}\varphi \\\partial _{x}\chi &\partial _{y}\chi &\partial _{z}\chi \end{pmatrix}}={\begin{pmatrix}{\frac {\cos(\varphi )}{\chi }}&{\frac {\sin(\varphi )}{\chi }}&-{\frac {\gamma }{\chi }}\\-{\frac {\sin(\varphi )}{\chi \gamma }}&{\frac {\cos(\varphi )}{\chi \gamma }}&0\\0&0&1\end{pmatrix}}}
Matriks transformasi diperlukan untuk mentransformasikan unit vektor dan bidang vektor. Matriks ini terdiri dari vektor satuan dari parameterisasi sebagai vektor kolom. Rincian lebih lanjut dapat ditemukan di bawah artikel Basiswechsel .
S
=
(
e
γ
→
e
φ
→
e
χ
→
)
=
(
cos
(
φ
)
−
sin
(
φ
)
γ
cos
(
φ
)
1
+
γ
2
sin
(
φ
)
cos
(
φ
)
γ
sin
(
φ
)
1
+
γ
2
0
0
1
1
+
γ
2
)
S
−
1
=
(
cos
(
φ
)
sin
(
φ
)
−
γ
−
sin
(
φ
)
cos
(
φ
)
0
0
0
1
+
γ
2
)
{\displaystyle S={\begin{pmatrix}{\overrightarrow {e_{\gamma }}}&{\overrightarrow {e_{\varphi }}}&{\overrightarrow {e_{\chi }}}\end{pmatrix}}={\begin{pmatrix}\cos(\varphi )&-\sin(\varphi )&{\frac {\gamma \cos(\varphi )}{\sqrt {1+\gamma ^{2}}}}\\\sin(\varphi )&\cos(\varphi )&{\frac {\gamma \sin(\varphi )}{\sqrt {1+\gamma ^{2}}}}\\0&0&{\frac {1}{\sqrt {1+\gamma ^{2}}}}\end{pmatrix}}\quad \quad \quad \quad S^{-1}={\begin{pmatrix}\cos(\varphi )&\sin(\varphi )&-\gamma \\-\sin(\varphi )&\cos(\varphi )&0\\0&0&{\sqrt {1+\gamma ^{2}}}\end{pmatrix}}}
Turunan parsial dapat ditransformasikan dengan matriks Jacobi terbalik
(
∂
∂
x
∂
∂
y
∂
∂
z
)
T
=
(
J
f
−
1
)
T
⋅
(
∂
∂
γ
∂
∂
φ
∂
∂
χ
)
T
{\displaystyle {\begin{pmatrix}{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\end{pmatrix}}^{T}=(J_{f}^{-1})^{T}\cdot {\begin{pmatrix}{\frac {\partial }{\partial \gamma }}&{\frac {\partial }{\partial \varphi }}&{\frac {\partial }{\partial \chi }}\end{pmatrix}}^{T}}
Hasilnya adalah:
∂
∂
x
=
cos
(
φ
)
χ
∂
∂
γ
−
sin
(
φ
)
γ
χ
∂
∂
φ
{\displaystyle {\frac {\partial }{\partial x}}={\frac {\cos(\varphi )}{\chi }}{\frac {\partial }{\partial \gamma }}-{\frac {\sin(\varphi )}{\gamma \chi }}{\frac {\partial }{\partial \varphi }}}
∂
∂
y
=
sin
(
φ
)
χ
∂
∂
γ
+
cos
(
φ
)
γ
χ
∂
∂
φ
{\displaystyle {\frac {\partial }{\partial y}}={\frac {\sin(\varphi )}{\chi }}{\frac {\partial }{\partial \gamma }}+{\frac {\cos(\varphi )}{\gamma \chi }}{\frac {\partial }{\partial \varphi }}}
∂
∂
z
=
∂
∂
χ
−
γ
χ
∂
∂
γ
{\displaystyle {\frac {\partial }{\partial z}}={\frac {\partial }{\partial \chi }}-{\frac {\gamma }{\chi }}{\frac {\partial }{\partial \gamma }}}
Vektor satuan dapat ditransformasikan dengan matriks transformasi terbalik.
(
e
x
→
e
y
→
e
z
→
)
=
(
e
γ
→
e
φ
→
e
χ
→
)
⋅
S
−
1
{\displaystyle {\begin{pmatrix}{\overrightarrow {e_{x}}}&{\overrightarrow {e_{y}}}&{\overrightarrow {e_{z}}}\end{pmatrix}}={\begin{pmatrix}{\overrightarrow {e_{\gamma }}}&{\overrightarrow {e_{\varphi }}}&{\overrightarrow {e_{\chi }}}\end{pmatrix}}\cdot S^{-1}}
Hasilnya adalah:
e
x
→
=
cos
(
φ
)
⋅
e
γ
→
−
sin
(
φ
)
⋅
e
φ
→
{\displaystyle {\overrightarrow {e_{x}}}=\cos(\varphi )\cdot {\overrightarrow {e_{\gamma }}}-\sin(\varphi )\cdot {\overrightarrow {e_{\varphi }}}}
e
y
→
=
sin
(
φ
)
⋅
e
γ
→
+
cos
(
φ
)
⋅
e
φ
→
{\displaystyle {\overrightarrow {e_{y}}}=\sin(\varphi )\cdot {\overrightarrow {e_{\gamma }}}+\cos(\varphi )\cdot {\overrightarrow {e_{\varphi }}}}
e
z
→
=
1
+
γ
2
⋅
e
χ
→
−
γ
⋅
e
γ
→
{\displaystyle {\overrightarrow {e_{z}}}={\sqrt {1+\gamma ^{2}}}\cdot {\overrightarrow {e_{\chi }}}-\gamma \cdot {\overrightarrow {e_{\gamma }}}}
Bidang vektor dapat ditransformasikan oleh perkalian matriks dengan matriks transformasi.
(
F
x
F
y
F
z
)
=
S
⋅
(
F
γ
F
φ
F
χ
)
{\displaystyle {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\end{pmatrix}}=S\cdot {\begin{pmatrix}F_{\gamma }\\F_{\varphi }\\F_{\chi }\end{pmatrix}}}
Hasilnya adalah:
F
x
=
cos
(
φ
)
⋅
F
γ
−
sin
(
φ
)
⋅
F
φ
+
γ
cos
(
φ
)
1
+
γ
2
⋅
F
χ
{\displaystyle F_{x}=\cos(\varphi )\cdot F_{\gamma }-\sin(\varphi )\cdot F_{\varphi }+{\frac {\gamma \cos(\varphi )}{\sqrt {1+\gamma ^{2}}}}\cdot F_{\chi }}
F
y
=
sin
(
φ
)
⋅
F
γ
+
cos
(
φ
)
⋅
F
φ
+
γ
sin
(
φ
)
1
+
γ
2
⋅
F
χ
{\displaystyle F_{y}=\sin(\varphi )\cdot F_{\gamma }+\cos(\varphi )\cdot F_{\varphi }+{\frac {\gamma \sin(\varphi )}{\sqrt {1+\gamma ^{2}}}}\cdot F_{\chi }}
F
z
=
1
1
+
γ
2
⋅
F
χ
{\displaystyle F_{z}={\frac {1}{\sqrt {1+\gamma ^{2}}}}\cdot F_{\chi }}
Diferensial permukaan dan volume
sunting
Diferensial volume dapat ditentukan menggunakan determinan dari matriks Jacobi. Ini menawarkan kemungkinan z. B. untuk menghitung volume kerucut menggunakan triple integral.
d
V
=
det
J
f
⋅
d
γ
d
χ
d
φ
=
χ
2
γ
⋅
d
γ
d
χ
d
φ
{\displaystyle dV=\det J_{f}\cdot d\gamma d\chi d\varphi =\chi ^{2}\gamma \cdot d\gamma d\chi d\varphi }
Diferensial permukaan dapat ditentukan dengan norma dari vektor normal permukaan. Jadi kamu bisa z. B. tentukan luas permukaan lateral dengan integral ganda.
d
A
=
‖
n
→
‖
⋅
d
χ
d
φ
=
χ
γ
1
+
γ
2
⋅
d
χ
d
φ
atau
γ
=
const.
{\displaystyle dA=\|{\overrightarrow {n}}\|\cdot d\chi d\varphi =\chi \gamma {\sqrt {1+\gamma ^{2}}}\cdot d\chi d\varphi \quad {\text{atau}}\quad \gamma ={\text{const.}}}
Operator diferensial vektor yang diubah
sunting
Representasi Operator Nabla dalam koordinat kerucut dapat diperoleh dengan memasukkan vektor satuan transformasi dan turunan parsial dalam operator kartesius Nabla:
∇
=
(
1
+
γ
2
χ
∂
∂
γ
−
γ
∂
∂
χ
)
⋅
e
γ
→
+
(
1
γ
χ
∂
∂
φ
)
⋅
e
φ
→
+
1
+
γ
2
(
∂
∂
χ
−
γ
χ
∂
∂
γ
)
⋅
e
χ
→
{\displaystyle \nabla =\left({\frac {1+\gamma ^{2}}{\chi }}{\frac {\partial }{\partial \gamma }}-\gamma {\frac {\partial }{\partial \chi }}\right)\cdot {\overrightarrow {e_{\gamma }}}+\left({\frac {1}{\gamma \chi }}{\frac {\partial }{\partial \varphi }}\right)\cdot {\overrightarrow {e_{\varphi }}}+{\sqrt {1+\gamma ^{2}}}\left({\frac {\partial }{\partial \chi }}-{\frac {\gamma }{\chi }}{\frac {\partial }{\partial \gamma }}\right)\cdot {\overrightarrow {e_{\chi }}}}
Gradien dalam koordinat kerucut diperoleh dengan menerapkan transformasi Operator Nabla ke medan skalar dalam koordinat kerucut.
grad
ϕ
=
∇
ϕ
=
(
1
+
γ
2
χ
∂
ϕ
∂
γ
−
γ
∂
ϕ
∂
χ
)
⋅
e
γ
→
+
(
1
γ
χ
∂
ϕ
∂
φ
)
⋅
e
φ
→
+
1
+
γ
2
(
∂
ϕ
∂
χ
−
γ
χ
∂
ϕ
∂
γ
)
⋅
e
χ
→
{\displaystyle \operatorname {grad} \phi =\nabla \phi =\left({\frac {1+\gamma ^{2}}{\chi }}{\frac {\partial \phi }{\partial \gamma }}-\gamma {\frac {\partial \phi }{\partial \chi }}\right)\cdot {\overrightarrow {e_{\gamma }}}+\left({\frac {1}{\gamma \chi }}{\frac {\partial \phi }{\partial \varphi }}\right)\cdot {\overrightarrow {e_{\varphi }}}+{\sqrt {1+\gamma ^{2}}}\left({\frac {\partial \phi }{\partial \chi }}-{\frac {\gamma }{\chi }}{\frac {\partial \phi }{\partial \gamma }}\right)\cdot {\overrightarrow {e_{\chi }}}}
Operator untuk divergensi bidang vektor dapat diperoleh dengan menerapkan operator Nabla ke bidang vektor dalam koordinat kerucut:
div
F
→
=
∇
⋅
F
→
=
1
γ
χ
⋅
(
∂
(
F
γ
⋅
γ
)
∂
γ
+
∂
F
φ
∂
φ
)
+
1
χ
2
1
+
γ
2
∂
(
F
χ
⋅
χ
2
)
∂
χ
{\displaystyle \operatorname {div} {\overrightarrow {F}}=\nabla \cdot {\overrightarrow {F}}={\frac {1}{\gamma \chi }}\cdot \left({\frac {\partial \left(F_{\gamma }\cdot \gamma \right)}{\partial \gamma }}+{\frac {\partial F_{\varphi }}{\partial \varphi }}\right)+{\frac {1}{\chi ^{2}{\sqrt {1+\gamma ^{2}}}}}{\frac {\partial \left(F_{\chi }\cdot \chi ^{2}\right)}{\partial \chi }}}
Definisi kerucut dapat diperluas ke dimensi yang lebih tinggi (lihat kerucut cembung ). Dalam hal ini, salah satu mengatakan bahwa cembung set C di nyata vektor ruang R n adalah kerucut (dengan puncaknya pada titik asal) jika untuk setiap vektor x di C dan setiap non-negatif bilangan real a , vektor kapak di C .[ 4]
^ a b Kesalahan pengutipan: Tag <ref> tidak sah;
tidak ditemukan teks untuk ref bernama :1 ^ Dale Varberg, Edward Purcell, Steve Rigdon (2006). Kalkulus Edisi Kesembilan, Jilid 1 . hlm. 282. (Penerjemah: I Nyoman Susila, Ph. D, Penerbit Erlangga)
^ (Protter & Morrey 1970 , hlm. 583)
^ Kesalahan pengutipan: Tag <ref> tidak sah;
tidak ditemukan teks untuk ref bernama grunbaum
![{\displaystyle V={\frac {\pi r^{2}}{h^{2}}}\int _{0}^{h}x^{2}\,\mathrm {d} x={\frac {\pi r^{2}}{h^{2}}}\left[{\frac {x^{3}}{3}}\right]_{0}^{h}={\frac {1}{3}}\pi r^{2}h}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a23fe16456b671453ff035b248ad53e0a2d565)
![{\displaystyle [0,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbede90a8f7ff59267c875f09e715c896ce7a51a)
