Menit busur

Menit busur (arcmin), dilambangkan dengan simbol ′, adalah satuan ukuran sudut yang sama dengan 160 dari satu derajat. Karena satu derajat adalah 1360 dari satu putaran (atau putaran penuh), maka satu menit busur adalah 121.600 dari satu putaran. Satu menit busur adalah π10.800 dari satu radian.

Menit busur
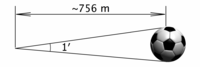Ilustrasi ukuran menit busur (bukan skala). Sebuah bola sepak standar (dengan diameter 22 cm atau 8,7 inci) membentuk sudut 1 menit busur pada jarak kira-kira 756 m (827 yard).
Informasi umum
Sistem satuan	Satuan non-SI yang disebutkan dalam SI
Besaran	Sudut
Simbol	′ atau arcmin
Dalam satuan	Tanpa dimensi dengan panjang busur kira-kira. ≈ 0.29091000 dari jari-jari, yakni 0.2909 mmm
Konversi
1 ′ dalam ...	... sama dengan ...
derajat	160° = 0.016°
detik busur	60″
radian	π10800 ≈ 0.000290888 rad
miliradian	π·100010800 ≈ 0.2909 mrad
gradian	6009g = 66.6g
putaran	121600

Aplikasi

Senjata api

Menit busur digunakan dalam industri senjata api, terutama senjata api jarak jauh, dalam menentukan akurasi laras tembakan. Dalam industri sejata api terdap istilah minute of angle di mana satu MOA kira-kira satu inci tinggi pada jarak 100 yard dari penembak. Seperdelapan MOA berarti seperdelapan inci pada jarak 100 yard atau satu inci pada jarak 800 yard. Penembak dapat dengan mudah mengatur telescopic sight yang berada di atas laras, menyesuaikan terhadap jarak tembaknya.

Dalam satuan metrik, satu MOA pada 100 meter adalah 2,908 cm.

Kartogafi, navigasi, dan surveying

Menit busur (dan satuan yang lebih kecil, detik busur) juga digunakan dalam kartografi dan navigasi pelayaran. Di permukaan laut, satu busur menit di sekitar ekuator setara dengan 1,86 km atau 1,15 mil (1 mil laut). Detik sudut adalah 1/60 dari angka tersebut, yaitu sekitar 30 meter atau 100 kaki. Pada umumnya sulit menentukannya secara akurat dikarenakan bentuk bumi yang tidak benar-benar bulat.

Pada kegiatan surveying, pembatasan suatu area juga umumnya menggunakan menit busur (dan detik busur jika membutuhkan akurasi tinggi). Kegiatan ini berhubungan dengan kartografi di mana penggunaannya menggunakan koordinat garis lintang dan garis bujur. Untuk penunjukan terhadap suatu titik dalam suatu peta, umumnya hanya menggunakan koordinat titik, misal 67^o 44' 4 Lintang Utara 35^o 13' 45 Bujur Barat. Cara lainnya dengan menggunakan arah dari suatu garis dalam garis lintang, misal Utara 65^o 39' 18 Barat 85.69 feet, berarti untuk menemukan titik tersebut maka kita harus berjalan sejauh 85,69 kaki ke arah barat dari 65^o 39' 18 lintang utara.

Pada penunjukkan terhadap suatu daerah yang relatif luas, koordinat menggunakan dua titik yang menjadi sudut-sudut yang saling berlawanan dari bidang persegi yang membatasi wilayah tersebut. Misalnya 50^o 5' Lintang Utara 13^o 67' Bujur Barat hingga 55^o 20' Lintang Utara 21^o 66' Bujur Barat. Selain itu, koordinat suatu wilayah yang luas juga bisa ditentukan dengan garis terpanjang yang melintang dan membujur melintasi wilayah tersebut. Misal, 40^o 30' Lintang Utara hingga 45^o 1' Lintang Utara dan 71^o 51' Bujur Barat hingga 79^o 46' Bujur Barat.

Astronomi

Menit busur dan detik busur juga digunakan dalam astronomi. Derajat dan juga menit busur digunakan untuk mengukur kemiringan atau jarak anguler dari utara atau selatan terhadap ekuator. Detik busur juga sering kali disebut dengan parsec, yang merupakan perpanjangan parallax second. Paralaks adalah kesalahan dalam melihat suatu benda atau pengukuran akibat kesalahan sudut pandang atau adanya pembiasan dari instrumen pengukuran dan media transmisi cahaya. Disebut parallax second karena benda langit senantiasa berubah posisinya terhadap pengamat akibat rotasi dan revolusi bumi.

Parsec hanyalah jarak relatif perpindahan benda langit terhadap pengamat akibat pergerakan bumi. Jika benda langit benar-benar bergerak sejauh satu parsec sedangkan pengamat diam, maka benda langit tersebut telah bergerak sejauh 3,26 tahun cahaya, atau sekitar 31 triliun kilometer.

Lihat pula

• Menit dan detik busur

Referensi

• Princeton.edu
• Wheeler R. E. Statistical notes on rifle group patterns. Diarsipkan 2006-09-26 di Wayback Machine. Diunduh 21 Mei 2009