Notasi ilmiah
Notasi ilmiah atau bisa disebut dengan notasi saintifik adalah cara penulisan nomor yang mengakomodasi bilangan yang memiliki nilai-nilai yang terlalu besar atau terlalu kecil untuk dengan mudah ditulis dalam notasi desimal standar pada umumya. Notasi ilmiah memiliki sejumlah sifat yang berguna dan umumnya digunakan dalam kalkulator oleh para ilmuwan, matematikawan, dokter, pecinta googologi, astronom dan insinyur.
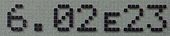
Dalam notasi ilmiah, semua nomor ditulis seperti dibawah ini:
("a dikali 10 pangkat b"), dengan pangkat b sebagai bilangan bulat, dan koefisien a adalah bilangan riil. Bilangan bulat a disebut eksponen dan bilangan riil b disebut significand(penanda) atau mantissa.[1] Jika nomor itu negatif, simbol negatif () diletakkan di depan simbol , seperti notasi desimal biasa. Dalam notasi normalisasi, penulisan dilakukan harus dengan memberi nilai pada variabel lebih atau sama dengan 1 namun kurang dari 10 ().
Notasi normalisasi
suntingDalam notasi normalisasi, penulisan notasi ilmiah dilakukan dengan memilih nilai agar nilai absolut dari lebih atau sama dengan 1, namun kurang dari 10 ( ). Misalnya: 300 akan ditulis sebagai dalam notasi ilmiah yang dinormalisasi, 14.285 akan ditulis sebagai . Jika nilai bilangan berada di antara 0 dan 1, maka nilai bernilai negatif. Misalnya, nilai 0.75 akan ditulis sebagai . Selain itu, angka 10 dan eksponennya biasanya dihilangkan jika nilai eksponen bernilai 0, sebagai contoh: . Proses normalisasi notasi dapat mempermudah dalam perbandingan beberapa nilai karena dapat cukup membandingkan nilai dari pangkatnya saja.
Notasi teknik
suntingDalam notasi teknik, penulisan notasi ilmiah dilakukan dengan memilih nilai dalam kelipatan 3, yang berarti nilai absolut berada di antara 1 dan 1000 ( ). Hal ini dilakukan agar penulisan angka sesuai dengan awalan SI yang dapat mempermudah komunikasi oral maupun pembacaan. misalnya, m dapat dibaca sebagai "dua belas koma lima nanometer" atau dapat ditulis sebagai 12,5 nm. Penulisan notasi ilmiah yang dinormalisasi untuk angka tersebut adalah m yang dapat dibaca sebagai "satu koma dua lima kali sepuluh pangkat negatif 8 meter."
| Notasi desimal biasa | Notasi teknik |
|---|---|
| 3.000 | 3×103 |
| 30.000 | 30×103 |
| 300.000 | 300×103 |
| 4.500.000 | 4,5×106 |
| 500.720.000.000 | 500,72×109 |
| 0,000000010675 | 10,675×10−12 |
| 0,000000100675 | 1,00675×10−12 |
Notasi E
sunting| Notasi ilmiah standar | Notasi E |
|---|---|
| 2×100 | 2E0
|
| 3×102 | 3E2
|
| 4,321768×103 | 4.321768E3
|
| −5,3×104 | -5.3E4
|
| 6,72×109 | 6.72E9
|
| 2×10−1 | 2E-1
|
| 9,87×102 | 9.87E2
|
| 7,51×10−9 | 7.51E-9
|
Kalkulator dan program komputer biasanya menampilkan angka yang sangat besar atau kecil menggunakan notasi ilmiah, dan beberapa program dapat dikonfigurasikan untuk menampilkan semua angka dengan cara tersebut. Karena eksponen pangkat seperti 107 dapat merepotkan untuk ditampilkan atau diketik, huruf "E" atau "e" (eksponen) sering digunakan untuk mewakili "a Dikalikan sepuluh pangkat b", sehingga dimana desimal ditulis sebagai a dan eksponen bilangan bulat sebagai b berarti sama dengan a × 10b. Sebagai contoh 6,022 × 1023 ditulis sebagai 6,022E23 atau 6,022e23, dan 1,6 × 10-35 ditulis sebagai 1,6E-35 atau 1,6e-35. Meskipun umum digunakan pada keluaran komputer, versi notasi ilmiah yang disingkat ini tidak disarankan untuk dokumen yang dipublikasikan oleh beberapa panduan gaya penulisan.[2]
Sebagian besar bahasa pemrograman populer - termasuk Fortran, C/C++, Python, dan JavaScript - menggunakan notasi "E" ini, yang berasal dari Fortran dan hadir dalam versi pertama yang dirilis untuk IBM 704 pada tahun 1956.[3] Notasi E telah digunakan oleh para pengembang SHARE Operating System (SOS) untuk IBM 709 pada tahun 1958.[4] Versi Fortran yang lebih baru (setidaknya sejak FORTRAN IV pada tahun 1961) juga menggunakan "D" untuk menandakan angka presisi ganda dalam notasi ilmiah,[5] dan kompiler Fortran yang lebih baru menggunakan "Q" untuk menandakan presisi empat kali lipat.[6] Bahasa pemrograman MATLAB mendukung penggunaan "E" atau "D".
Bahasa pemrograman ALGOL 60 (1960) menggunakan karakter subskrip sepuluh "10" sebagai pengganti huruf "E" pada notasi ini, misalnya: 6.0221023.[7][8] Hal ini menjadi tantangan bagi sistem komputer yang tidak menyediakan karakter tersebut, sehingga ALGOL W (1966) mengganti simbol tersebut dengan tanda kutip tunggal, misalnya 6.022'+23, dan beberapa varian Algol Soviet mengizinkan penggunaan huruf Sirilik "ю", misalnya 6.022ю + 23. Selanjutnya, bahasa pemrograman ALGOL 68 menyediakan pilihan karakter: E, e, \, ⊥, atau 10. Karakter ALGOL "10" dimasukkan dalam pengkodean teks GOST 10859 Soviet (1964), dan ditambahkan ke Unicode 5.2 (2009) sebagai U+23E8 ⏨ simbol eksponan desimal.
Angka-angka Penting
suntingAngka-angka penting adalah angka dalam bilangan yang menambah ketepatan nilai bilangan tersebut. Ini mencakup semua angka yang bukan nol, angka nol di antara angka penting, dan angka nol yang diindikasikan sebagai angka penting. Angka nol di depan dan di belakangnya bukanlah angka penting, karena angka tersebut hanya ada untuk menunjukkan skala angka. Sayangnya, hal ini menyebabkan ambiguitas. Angka 1.230.400 biasanya dibaca memiliki lima angka penting: 1, 2, 3, 0 dan 4. Dua angka nol terakhir hanya berfungsi sebagai penunjuk seberapa besar nilai angka itu dan tidak menambah ketepatan.
Ketika sebuah bilangan dikonversi ke dalam notasi ilmiah dengan cara dinormalisasi, koefisien dari bilangan tersebut diperkecil menjadi angka antara 1 dan 9,999... Semua angka penting tetap ada, tetapi angka nol di belakang koma tidak lagi diperlukan. Dengan demikian, bilngan 1.230.400 akan diubah menjadi 1,2304×106 jika memiliki lima digit signifikan. Jika angka tersebut diketahui memiliki enam atau tujuh angka penting, angka tersebut akan ditampilkan sebagai 1,23040 × 106 atau 1,230400 × 106. Perlu diingat bahwa angka nol dibelakang maupun didepan angka penting tidak dianggap dan tidak merubah nilai dari suatu bilangan. Dengan demikian, tambahan angka pada notasi ilmiah tidak menjadi ambigu.[Butuh rujukan]
Penaksiran nilai angka terakhir
suntingSudah menjadi kebiasaan dalam pengukuran ilmiah untuk mencatat semua angka yang diketahui secara pasti dari pengukuran dan memperkirakan setidaknya satu angka tambahan jika ada informasi yang tersedia mengenai nilainya. Bilangan yang dihasilkan mengandung lebih banyak informasi daripada tanpa angka tambahan, yang dapat dianggap sebagai angka penting karena menyampaikan beberapa informasi yang mengarah pada presisi yang lebih besar dalam pengukuran dan dalam agregasi pengukuran (menambahkan atau mengalikannya).
Informasi tambahan tentang presisi dapat disampaikan melalui notasi tambahan. Sering kali berguna untuk mengetahui seberapa tepat angka atau digit terakhir. Sebagai contoh, nilai massa proton yang diterima dapat dinyatakan dengan tepat sebagai 1.67262192369(51)×10-27 kg, yang merupakan singkatan dari (1.67262192369±0.00000000051)×10-27 kg. Namun, masih belum jelas apakah kesalahan (5,1 × 10-37 dalam kasus ini) adalah kesalahan maksimum yang mungkin terjadi, kesalahan standar, atau patokan lainnya.
Penggunaan spasi
suntingDalam notasi ilmiah yang dinormalisasi, dalam notasi E, dan dalam notasi teknik, spasi (yang dalam penyusunan huruf dapat diwakili oleh spasi lebar normal atau spasi tipis) yang hanya diperbolehkan sebelum dan sesudah "×" atau di depan "E" terkadang dihilangkan, meskipun kurang umum untuk melakukannya sebelum karakter abjad.
Contoh-contoh lain dalam penggunaan notasi ilmiah
sunting- Massa sebuah elektron adalah sekitar 0,000000000000000000000000000000910938356 kg.[9] Dalam notasi ilmiah, ini dituliskan 9,10938356×10-31 kg.
- Massa Bumi adalah sekitar 5.972.400.000.000.000.000.000.000 kg. Dalam notasi ilmiah, ini dituliskan 5,9724×1024 kg.[10]
- Keliling Bumi adalah sekitar 40.000.000 m.[11] Dalam notasi ilmiah, ini adalah 4 × 107 m. Dalam notasi teknik, ini ditulis 40 × 106 m. Dalam gaya penulisan SI, ini dapat ditulis 40 Mm (40 megameter).
- Satu inci didefinisikan sebagai 25,4 mm. Dengan menggunakan notasi ilmiah, nilai ini dapat dinyatakan secara seragam dengan presisi yang diinginkan, dari sepersepuluh milimeter terdekat 2,54 × 101 mm hingga nanometer terdekat 2,5400000 × 101 mm, atau lebih.
- Hiperinflasi berarti terlalu banyak uang yang beredar, mungkin dengan mencetak uang kertas, mengejar barang yang terlalu sedikit. Kadang-kadang didefinisikan sebagai inflasi 50% atau lebih dalam satu bulan. Dalam kondisi seperti itu, uang dengan cepat kehilangan nilainya. Beberapa negara pernah mengalami inflasi sebesar 1 juta persen atau lebih dalam satu bulan, yang biasanya mengakibatkan mata uang tersebut ditinggalkan dengan cepat. Sebagai contoh, pada bulan November 2008, tingkat inflasi bulanan dolar Zimbabwe mencapai 79,6 miliar persen; perkiraan nilai dengan tiga angka penting adalah 7,96×1010%, atau lebih mudahnya adalah 7,96×108.[12][13]
Konversi ke dalam bentuk desimal
suntingMengonversi angka dalam kasus ini berarti mengubah angka ke dalam bentuk notasi ilmiah, mengubahnya kembali ke dalam bentuk desimal, atau mengubah bagian eksponen dari persamaan. Tidak satu pun dari hal ini yang mengubah angka sebenarnya, hanya cara menyatakannya.
Desimal ke ilmiah
suntingmerubah angka desimal menjadi ilmiah dapat dilakukan juga dengan menggunakan bantuan komputer, namun dapat juga dilakukan secara mandiri dengan langkah langkah berikut:
Identifikasi Angka Penting (a):
sunting- Temukan angka non-nol pertama dalam bilangan desimal yang akan dikonversi. Ini akan menjadi angka awal dalam notasi ilmiah, lalu temukan angka lainnya yang bukan angka nol, angka nol diantara angka penting atau angka nol yang diidentifikasi sebagai angka penting.
- Contoh: Untuk 0,000000010675, angka penting pertama adalah 1. Angka penting lainnya adalah 0,6,7,5; angka nol didalam kasus ini dianggap penting karena berada diantara angka penting lainnya.
Pindahkan Titik Desimal:
sunting- Pindahkan titik desimal ke posisi setelah angka non-nol pertama yang Anda temukan, dan hitung berapa banyak langkah Anda harus memindahkannya.
- Contoh: Anda memindahkan angka-angka penting tadi sebanyak 8 tempat ke kanan untuk mengubah 1,0675 menjadi 0,000000010675.
Tentukan Eksponen (b):
sunting- Eksponen b adalah jumlah langkah Anda memindahkan angka penting.
- Jika Anda memindahkan titik desimal ke kanan, eksponen b adalah negatif.
- Jika Anda memindahkan titik desimal ke kiri, eksponen b adalah positif.
- Contoh: Karena Anda memindahkan titik desimal 8 tempat ke kanan, eksponennya adalah −8.
Susun dalam Notasi Ilmiah:
sunting- Notasi ilmiah dari bilangan tersebut adalah a×10b.
- Contoh: Hasilnya adalah 1,0675×10−8.
Untuk menyederhanakan, Anda biasanya membulatkan angka penting a hingga beberapa digit saja, tergantung pada kebutuhan presisi.
Contoh: Bilangan 0,000000010675 menjadi 1,0675−8 atau 1,07×10−8 jika dibulatkan ke dua angka penting.
Ilmiah ke desimal
suntingUntuk mengubah angka dari notasi ilmiah ke notasi desimal, pertama-tama hilangkan × 10n di bagian akhir, lalu geser pemisah desimal n digit ke kanan (n positif) atau ke kiri (n negatif). Angka 1,2304×106 akan memiliki pemisah desimal yang digeser 6 digit ke kanan dan menjadi 1.230.400,0 sedangkan -4,0321×10-3 akan memiliki pemisah desimal yang digeser 3 digit ke kiri dan menjadi -0,0040321.1.234×103 = 12.34×102 = 123.4×101 = 1234
Operasi dasar
suntingBilangan yang berbentuk notasi ilmiah yang dinormalisasi dapat langsung dikalikan atau dibagi dengan bilangan yang dinormalisasi yang lain, perkalian bilangan ilmiah normalisasi dapat dilakukan menggunakan rumus sebagai berikut:
Dimana:
Contoh perkalian notasi ilmiah normalisasi:
Sedangkan untuk pembagian bilangan dalam notasi ilmiah normalisasi dapat dilakukan juga dengan rumus berikut:
Dimana:
Contoh pembagian notasi ilmiah normalisasi:
Sedangkan untuk menjumlahkan atau mengurangi, nilai eksponen harus disamakan antara kedua bilangan sebelum dilakukannya penjumlahan atau pengurangan.
Lihat pula
suntingReferensi
sunting- ^ "Scientific notation". Wikipedia (dalam bahasa Inggris). 2024-05-21.
- ^ Edward, John (2009). Submission Guidelines for Authors: HPS 2010 Midyear Proceedings (PDF). McLean, VA: Health Physics Society. p. 5.
- ^ However, E notation was not included in the preliminary specification of Fortran, as of 1954.
Backus, John Warner, ed. (1954-11-10). Specifications for: The IBM Mathematical FORmula TRANSlating System, FORTRAN (PDF) (Preliminary report). New York: Programming Research Group, Applied Science Division, International Business Machines Corporation. Diakses tanggal 2022-07-04. (29 pages)
Sayre, David, ed. (1956-10-15). The FORTRAN Automatic Coding System for the IBM 704 EDPM: Programmer's Reference Manual (PDF). New York: Applied Science Division and Programming Research Department, International Business Machines Corporation. hlm. 9, 27. Diakses tanggal 2022-07-04. (2+51+1 pages)
- ^ DiGri, Vincent J.; King, Jane E. (April 1959). "The SHARE 709 System: Input-Output Translation". Journal of the ACM. 6 (2): 141–144. doi:10.1145/320964.320969 .
It tells the input translator that the field to be converted is a decimal number of the form ~X.XXXXE ± YY where E implies that the value of ~x.xxxx is to be scaled by ten to the ±YY power.
(4 pages) (NB. This was presented at the ACM meeting 11–13 June 1958.) - ^ "Fortran: Lesson 3 | Department of Mathematics" (dalam bahasa Inggris). 2011-10-09. Diakses tanggal 2024-08-10.
- ^
For instance, DEC FORTRAN 77 (f77), Intel Fortran, Compaq/Digital Visual Fortran, and GNU Fortran (gfortran)
"Double Precision, REAL**16". DEC Fortran 77 Manual. Digital Equipment Corporation. Diakses tanggal 2022-12-21.
Digital Fortran 77 also allows the syntax Qsnnn, if the exponent field is within the T_floating double precision range. […] A REAL*16 constant is a basic real constant or an integer constant followed by a decimal exponent. A decimal exponent has the form: Qsnn […] s is an optional sign […] nn is a string of decimal digits […] This type of constant is only available on Alpha systems.
Intel Fortran: Language Reference (PDF). Intel Corporation. 2005. hlm. 3–7–3–8, 3–10. 253261-003. Diakses tanggal 2022-12-22. (858 pages) Compaq Visual Fortran – Language Reference (PDF). Houston: Compaq Computer Corporation. August 2001. Diakses tanggal 2022-12-22. (1441 pages)"6. Extensions: 6.1 Extensions implemented in GNU Fortran: 6.1.8 Q exponent-letter". The GNU Fortran Compiler. 2014-06-12. Diakses tanggal 2022-12-21.
- ^ Naur, Peter, ed. (1960). Report on the Algorithmic Language ALGOL 60. Copenhagen.
- ^ Savard, John J. G. (2018). "Computer Arithmetic". quadibloc. The Early Days of Hexadecimal. Diakses tanggal 2018-07-16.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (July–September 2016). "CODATA recommended values of the fundamental physical constants: 2014". Reviews of Modern Physics. 88 (3): 035009. arXiv:1507.07956 . Bibcode:2016RvMP...88c5009M. CiteSeerX 10.1.1.150.1225 . doi:10.1103/RevModPhys.88.035009.
- ^ Luzum, Brian; Capitaine, Nicole; Fienga, Agnès; Folkner, William; Fukushima, Toshio; Hilton, James; Hohenkerk, Catherine; Krasinsky, George; Petit, Gérard; Pitjeva, Elena; Soffel, Michael; Wallace, Patrick (August 2011). "The IAU 2009 system of astronomical constants: The report of the IAU working group on numerical standards for Fundamental Astronomy". Celestial Mechanics and Dynamical Astronomy. 110 (4): 293–304. Bibcode:2011CeMDA.110..293L. doi:10.1007/s10569-011-9352-4 .
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (July–September 2016). "CODATA recommended values of the fundamental physical constants: 2014". Reviews of Modern Physics. 88 (3): 035009. arXiv:1507.07956 . Bibcode:2016RvMP...88c5009M. CiteSeerX 10.1.1.150.1225 . doi:10.1103/RevModPhys.88.035009.
- ^ Kadzere, Martin (2008-10-09). "Zimbabwe: Inflation Soars to 231 Million Percent". Harare, Zimbabwe: The Herald. Diakses tanggal 2008-10-10.
- ^ "Zimbabwe inflation hits new high". BBC News. 9 October 2008. Diarsipkan dari versi asli tanggal 2009-05-14. Diakses tanggal 2009-10-09.



